Very good. WSM can undoubtedly be used for this type of problems. The original discussion however was about the benefits of OOP as compared to classic functional programming. OOP is indeed many times faster and he can introduce hundreds of pendulums and still have a fast animation. The number is absurd but Kobayashi was making a key point: OOP is very, very much faster, at least in this case. Some experts on OOP will understand why? My functional program example is limited to some 10 pendulums beyond that, speed becomes an issue. I do not know if WSM would give similar speed benefits?

Fantastic application! Thanks for sharing this.

Another way to observe this phenomenon could be using Wolfram SystemModeler. Here I have constructed a double pendulum model in SystemModeler (model is attached):

Like your application, the underlying language of SystemModeler is object oriented. This allows all the components you see above be extended into arrays of components. By setting a parameter "n", the number of pendulums can be selected.

Using Mathematica, we can set the initial angles of the different pendulums to have very small deviations:

Needs["WSMLink`"]

n = 10;

WSMSetValues["DoublePendulum", {"n" -> n}];
WSMSetValues[
  "DoublePendulum", {"revolute2.phi" -> 
    RandomReal[{-10^-12 Degree, 10^-12 Degree}, n]}, "InitialValues"];

The result will look something like this:

Video courtesy of @Neil Singer

Attachments:

Hi, Mahieu,

Your project is intending centuple pendulum motion equation! Great! I hope the OOP can help your project, however, i have no idea on your Falling Chain code now. But, if there was a bottleneck on the drawing graphics, OOP may support the speedup for the graphics with representing each pendulum as a instance of graphics class.

I'm very grad you did understand my OOP idea well. Thank you.

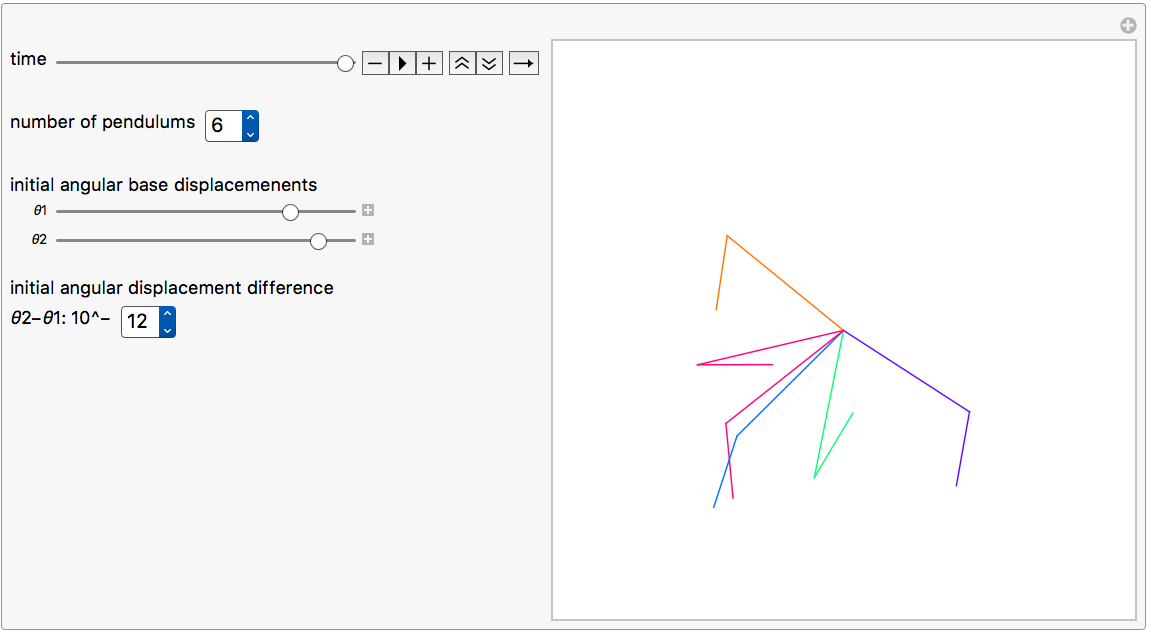
I am very interested in your subject of chaos and the double pendulum. Your implementation with OOP was a surprise but I figured it out and I was able to learn a lot about UpValues, Upset, DelayedUpset etc... However, I do not understand what is the exact advantage of using your OOP paradigm. I did the same using ParametricNDSolve and implemented your formulas without any problem.

Manipulate[
 Quiet@Module[{T1, T2, V1, V2, L, lkeq, 
    ans, \[Theta]1Eff, \[Theta]2Eff, pendulum, butterfly, g = 9.8, 
    m = 1, r1 = 1, r2 = 0.5},
   SeedRandom[13];
   (*Lagrangian setup*)
   T1 = 1/2 m*r1^2*\[Theta]1'[t]^2;
   V1 = -m*g*r1*Cos[\[Theta]1[t]];
   T2 = 1/
      2 m*(r1^2*\[Theta]1'[t]^2 + r2^2*\[Theta]2'[t]^2 + 
       2 r1*r2*\[Theta]1'[t]*\[Theta]2'[t]*r1*r2*
        Cos[\[Theta]1[t] - \[Theta]2[t]]);
   V2 = -m*g*(r1*Cos[\[Theta]1[t]] + r2*Cos[\[Theta]2[t]]);
   L = T1 + T2 - (V1 + V2);
   (*Lagrange equation of motion*)
   lkeq = {D[D[L, \[Theta]1'[t]], t] - D[L, \[Theta]1[t]] == 0, 
     D[D[L, \[Theta]2'[t]], t] - D[L, \[Theta]2[t]] == 0};
   (*Numerical solve parametric differential equation: 
   parameter is the initial angular displacement increment*)
   ans = ParametricNDSolve[{lkeq, {\[Theta]1[0] == 
        th1 + \[Epsilon], \[Theta]2[0] == 
        th2 + \[Epsilon], \[Theta]1'[0] == 0, \[Theta]2'[0] == 
        0}}, {\[Theta]1, \[Theta]2}, {t, 0, time}, {\[Epsilon]}, 
     MaxSteps -> \[Infinity], PrecisionGoal -> \[Infinity]];
   \[Theta]1Eff[\[Epsilon]_, tr_] := \[Theta]1[\[Epsilon]][tr] /. 
     ans;
   \[Theta]2Eff[\[Epsilon]_, tr_] := \[Theta]2[\[Epsilon]][tr] /. ans;
    butterfly = 10^-pwr;
   pendulum[\[Epsilon]_, col_: Black] := {col, 
     Line[{{0, 
        0}, {r1*Sin[\[Theta]1Eff[\[Epsilon], tr]], -r1*
         Cos[\[Theta]1Eff[\[Epsilon], tr]]}}], 
     Line[{{r1*Sin[\[Theta]1Eff[\[Epsilon], tr]], -r1*
         Cos[\[Theta]1Eff[\[Epsilon], tr]]}, {(r1*
           Sin[\[Theta]1Eff[\[Epsilon], tr]] + 
          r2*Sin[\[Theta]2Eff[\[Epsilon], tr]]), (-r1*
           Cos[\[Theta]1Eff[\[Epsilon], tr]] - 
          r2*Cos[\[Theta]2Eff[\[Epsilon], tr]])}}]};
   (*-----graphics display--------*)

   Graphics[
    Map[pendulum[butterfly*#1, Hue[#1]] &, RandomReal[{-1, 1}, n]], 
    PlotRange -> {{-1.8, 1.8}, {-1.8, 1.8}}]],
 (*-----controls--------*)
 {{tr, 0, Style["time", 12]}, 0, time, 
  Animator, AnimationRunning -> False, AnimationRepetitions -> 1, 
  AnimationRate -> .025},
 Row[{Style["\nnumber of pendulums", 12], 
   Control[{{n, 6, ""}, Range[12]}]}],
 Style["\ninitial angular base displacemenents", 
  12], {{th1, 2., "\[Theta]1"}, -3.14, 
  3.14}, {{th2, 2.5, "\[Theta]2"}, -3.14, 3.14},
 Row[{Style[
    "\ninitial angular displacement difference\n\[Theta]2-\[Theta]1: \
10^-", 12], Control[{{pwr, 12, ""}, Range[3, 16]}]}], {{time, 50}, 
  None},
 (*-----options--------*)
 TrackedSymbols :> Manipulate, 
 AutorunSequencing -> {}, ControlPlacement -> Left]

I further more could introduce a variable number of pendulums and a variable "butterfly" value. All this using plain functional programming. Your method is very elegant and smart but what exactly can one do more,faster or better with OOP?