I looked at this one more time but I believe that the MMA numerical result is correct. You can integrate the expression in eta for a given value of n and get a closed form solution. I added assumptions based on your range of interest until the equation simplified without Conditionals and without complex terms:

exp = 1/((t Sin[phi])^2 + r^2 + (t Cos[phi] + Z - z)^2 - 
     2 r t Sin[phi] Cos[eta])^n 
int1 = Integrate[ exp /. phi -> Pi/3 /. Z -> 0 /. n -> 3, {eta, 0, 2 Pi}, 
  Assumptions ->  z > 0 && z < 50 && t > 0 && r \[Element] Reals && 
    t \[Element] Reals && 
    z \[Element] Reals && -r^4 + r^2 (t^2 + 2 t z - 2 z^2) - (t^2 - t z + z^2)^2 <
      0 && r != 0 ]

The result is

(\[Pi] (2 r^4+2 (t^2-t z+z^2)^2+r^2 (7 t^2-4 t z+4 z^2)))/(r^4-r^2 (t^2+2 t z-2 z^2)+(t^2-t z+z^2)^2)^(5/2)

If you numerically integrate this in z and t you get the same answer. I think you can also now analytically integrate this wrt t and z. I did the indefinite integral quickly but the definite integral was taking a long time. Either way, you can plot the curve and see the area that you are trying to integrate:

Plot3D[r*int1 /. 
  MapThread[
   Rule, {{r, a, b, Z, A, B, phi}, {4.087, 1.205, 0.3812, 0, 345.0527,
      606741.04395, Pi/3}}], {z, 0, 50}, {t, -5/3, 5/3}, 
 PlotRange -> All]

which gives you this:

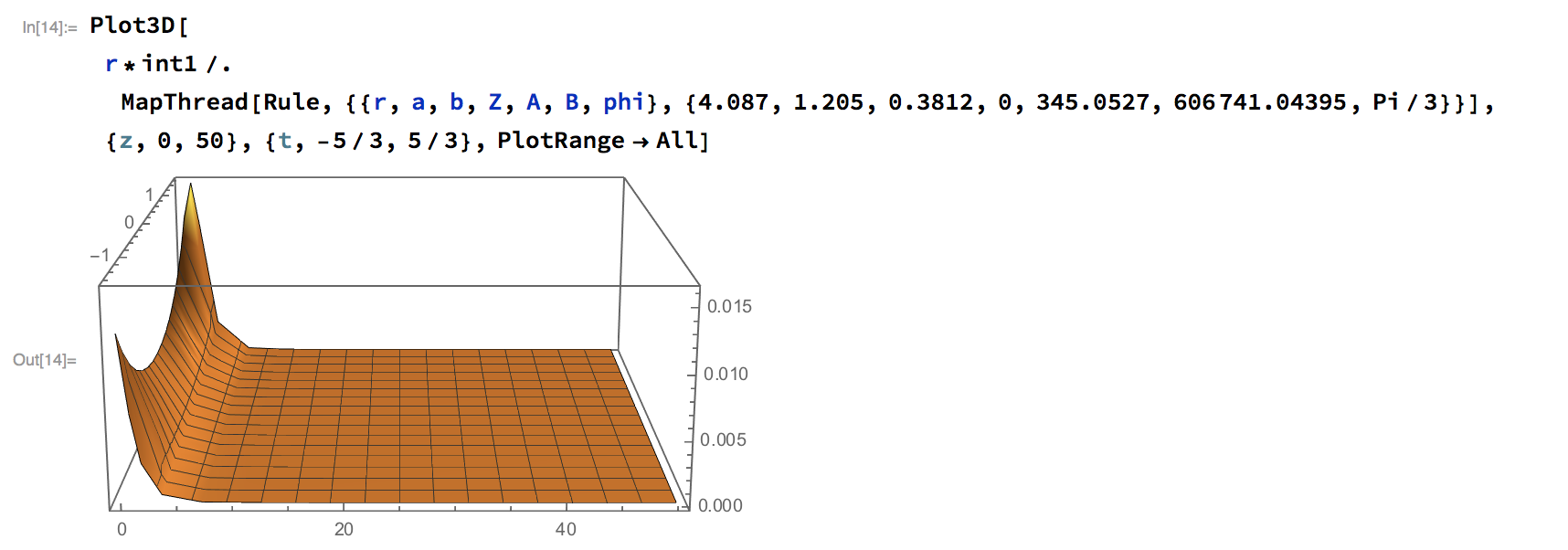
Note the curve is smooth and continuous -- there is nothing there that would cause integration problems. I know you do not want to accept this answer, however, it is unlikely for MMA, Matlab, and this analysis to all be simultaneously wrong with the same wrong answer. Isn't it more likely that the paper that was published has a typographical error?

If you really want to integrate the expression analytically, you can take the result that I got (which is a ratio of polynomials) and experiment some more in MMA (maybe take the indefinite integral and evaluate it yourself). Another viable option is to look up the integration formulas (for t and then z, or vice-versa). A good place to start is Gradshteyn and Ryzhik -- they will have many integrals that MMA cannot do. You can apply the formulas in MMA and analytically get your answer. I hope this helps.

Regards

Thank you for your kind cooperation. Is it possible to use symbolic integration using Integrate command. Using one of their two methods I am getting their answer. The one which I have asked here I am not getting their answer that makes me thinking there is some problem with result MMA is giving. The spikes consist of very small region and other space the function goes to zero. So I have a doubt that whether MMA correctly calculating it or Is it missing those spikes.I have read something about such cases.

The expression is of the form 1/(y^n). The expression only can blow up when y is close to zero. I solved for y= 0:

NSolve[((t Sin[phi])^2 + r^2 + (t Cos[phi] + Z - z)^2 - 
    2 r t Sin[phi] Cos[eta]) == 0, {t, z, eta}, Reals]

Which gave me three solutions:

{{t -> ConditionalExpression[-4.71926, C[1] \[Element] Integers], 
  z -> ConditionalExpression[-2.35963, C[1] \[Element] Integers], 
  eta -> ConditionalExpression[1. (-3.14159 + 6.28319 C[1]), 
    C[1] \[Element] Integers]}, 

{t ->   ConditionalExpression[-4.71926, C[1] \[Element] Integers], 
      z -> ConditionalExpression[-2.35963, C[1] \[Element] Integers], 
      eta -> ConditionalExpression[1. (3.14159 + 6.28319 C[1]), 
        C[1] \[Element] Integers]}, 

{t ->  ConditionalExpression[4.71926, C[1] \[Element] Integers], 
      z -> ConditionalExpression[2.35963, C[1] \[Element] Integers], 
      eta -> ConditionalExpression[6.28319 C[1], 
        C[1] \[Element] Integers]}}

Note that all of the solution are outside of your integration range so unless I missed something, your expression is continuous in your region. I also fixed eta and n-> 3 and plotted the expression:

Plot3D[1/((t Sin[phi])^2 + r^2 + (t Cos[phi] + Z - z)^2 - 
       2 r t Sin[phi] Cos[eta])^n /. eta -> 2 Pi /. n -> 3, {z, 0, 
  50}, {t, -5/3, 5/3}, PlotRange -> All]

It spikes to .003 and is mostly very small but the area under the curve seems calculable and smooth -- You can try different values and integrate it in a different program to check. Are you sure the original source does not have a slightly different parenthesis or a subtle difference?

I am also thinking the same. But when \phi=0 I get the same value as theirs which can rule out the possibility of a typo. How you came to a conclusion that it is smooth. Did you plot the function by keeping one of the integration variable as a constant. Is it possible to do a symbolic integration rather than numerical integration. I tried it but it takes too long which forced me to kill the job. For \phi=0 the computation time is very less compared for non zero \phi's and without any error messages.

Thank you. The answer is -2.00015 which is not matching with answer in the source from which I have taken this problem. The answer from their calculation is -4.4. I dont need 20 digits 5 or 6 is ok. but I am really confused with what is causing such a difference. Is it possible to evaluate it symbolically using Integrate command rather than numerical integration.

Thank you. The answer is -2.00015 which is not matching with answer in the source from which I have taken this problem. The answer from their calculation is -4.4. I dont need 20 digits 5 or 6 is ok. but I am really confused with what is causing such a difference. Is it possible to evaluate it symbolically using Integrate command rather than numerical integration.