I looked at this one more time but I believe that the MMA numerical result is correct. You can integrate the expression in eta for a given value of n and get a closed form solution. I added assumptions based on your range of interest until the equation simplified without Conditionals and without complex terms:
exp = 1/((t Sin[phi])^2 + r^2 + (t Cos[phi] + Z - z)^2 -
2 r t Sin[phi] Cos[eta])^n
int1 = Integrate[ exp /. phi -> Pi/3 /. Z -> 0 /. n -> 3, {eta, 0, 2 Pi},
Assumptions -> z > 0 && z < 50 && t > 0 && r \[Element] Reals &&
t \[Element] Reals &&
z \[Element] Reals && -r^4 + r^2 (t^2 + 2 t z - 2 z^2) - (t^2 - t z + z^2)^2 <
0 && r != 0 ]
The result is
(\[Pi] (2 r^4+2 (t^2-t z+z^2)^2+r^2 (7 t^2-4 t z+4 z^2)))/(r^4-r^2 (t^2+2 t z-2 z^2)+(t^2-t z+z^2)^2)^(5/2)
If you numerically integrate this in z and t you get the same answer. I think you can also now analytically integrate this wrt t and z. I did the indefinite integral quickly but the definite integral was taking a long time. Either way, you can plot the curve and see the area that you are trying to integrate:
Plot3D[r*int1 /.
MapThread[
Rule, {{r, a, b, Z, A, B, phi}, {4.087, 1.205, 0.3812, 0, 345.0527,
606741.04395, Pi/3}}], {z, 0, 50}, {t, -5/3, 5/3},
PlotRange -> All]
which gives you this:
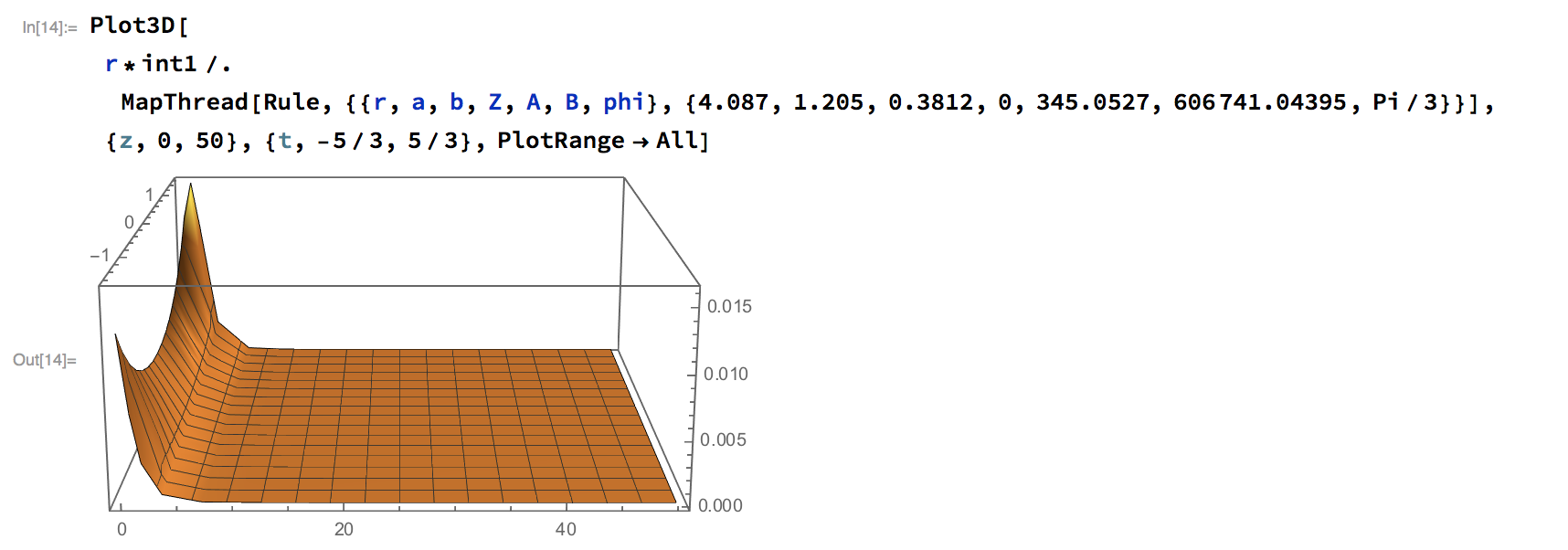
Note the curve is smooth and continuous -- there is nothing there that would cause integration problems. I know you do not want to accept this answer, however, it is unlikely for MMA, Matlab, and this analysis to all be simultaneously wrong with the same wrong answer. Isn't it more likely that the paper that was published has a typographical error?
If you really want to integrate the expression analytically, you can take the result that I got (which is a ratio of polynomials) and experiment some more in MMA (maybe take the indefinite integral and evaluate it yourself). Another viable option is to look up the integration formulas (for t and then z, or vice-versa). A good place to start is Gradshteyn and Ryzhik -- they will have many integrals that MMA cannot do. You can apply the formulas in MMA and analytically get your answer. I hope this helps.
Regards