Spin Around

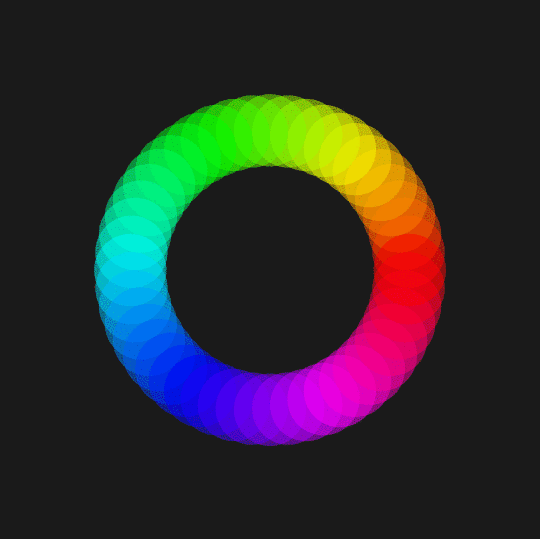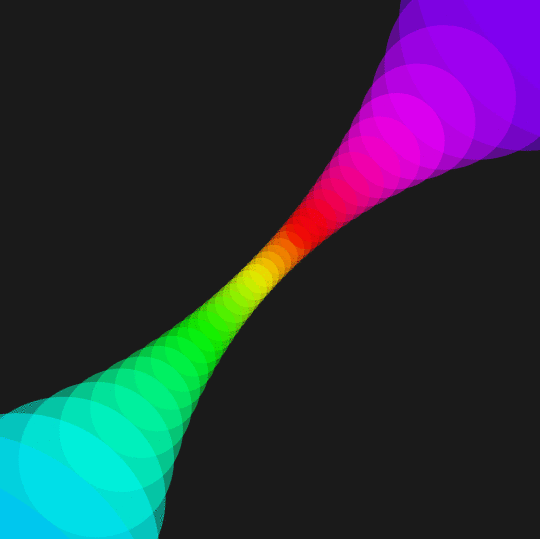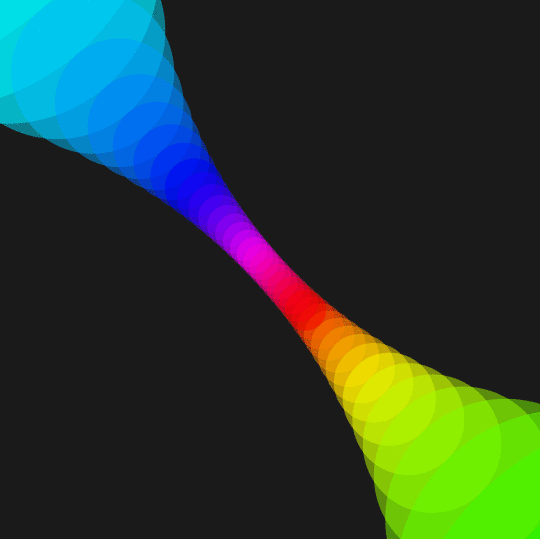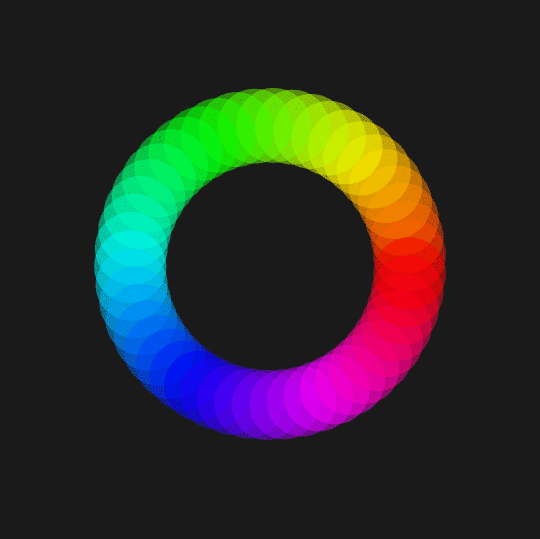
Like Interference, Dig In, and Tetra, this shows the stereographic projection of a collection of circles on the unit 2-sphere at constant distance from some chosen points. In this case, the circles up in the sphere all have (spherical) radius $\pi/12$; the points they're centered on are 48 equally-spaced points on the equator which are rotated around the axis $(-1,0,3/4)$.

To get a spherical circle centered on a point $p$, we can simply find an orthonormal basis

b = Orthogonalize[NullSpace[{p}]]

for the orthogonal complement and then parametrize the circle of radius $\phi$ by

Cos[?] p + Sin[?] (Cos[s] b[[1]] + Sin[s] b[[2]])

Now, we can define stereographic projection and implement the above idea:

Stereo[{x_, y_, z_}] := 1/(1 - z) {x, y};

DynamicModule[{p, b, ? = ?/12, n = 48},
 Manipulate[
  Graphics[{EdgeForm[None], Opacity[.5],
    Table[
     p = RotationMatrix[?, {-1, 0, 3/4}].{Cos[2 ? t/n], Sin[2 ? t/n], 0};
     b = Orthogonalize[NullSpace[{p}]];
     If[VectorAngle[p, {0, 0, 1}] > .36,
      {Hue[t/n],
       Polygon[
        Table[
         Stereo[Cos[?] p + Sin[?] (Cos[s] b[[1]] + Sin[s] b[[2]])],
         {s, 0, 2 ?, 2 ?/200}]]}],
     {t, 1., n}]},
   PlotRange -> 2, Frame -> False, Background -> GrayLevel[.1], 
   ImageSize -> 540],
  {?, 0, 2 ?}]
 ]

Note that the goofy If is to prevent circles from getting too near the north pole (in the plane, when a circles gets too close to infinity, it has an annoying habit of turning inside out).

Also, the above Manipulate looks fine in the notebook, but when I export the red circles are visually "above" the orange circles they're adjacent to (presumably because the red circles are at the end of the Table). To fix that for the final GIF, I put each circle in a separate Graphics object which I then combined with ImageCompose. It comes out nicer, but takes a lot longer.