Thanks Shenguhi,
I used Row [.] but not Control [.]
Now it works

The example is revealing.
That is a side effect and functional programming languages should not suffer from that. It is one of its main characteristics.

I will abuse your patience one more time, in Manipulate, can I arrange the controls in a row instead of columns?

Hello guys, Gianluca's code does the job.
I confess that I tried to avoid using Manipulate, for me it is very opaque and esoteric.
I still wonder why if I replace commas with semicolons the former code stops working
Semicolons are used to avoid the outs, are they?

Last question, I promise, how can I place the radio button to the right of the sliders?

Thank you very much for your help

Hi Gorni, Yes you are right. I believe Manipulate is the way to go also with all the other stuff Jorge wants to do around it.

Yes, it works great.

But if I change the commas by semicolons it does not work.

Is there any way to hide the intermediate results in the notebook? I mean just show the Grid

Hello I van,

I want to generate two queues (qc and pc) of random numbers. Each queue should be generated "just in time" when the user manipulates the corresponding slider.

The queues will be used in a simulation system and the grid is a simplification of the actual output. It is important that the simulation be carried out with the same random numbers shown in the Grid.

Generating a larger list and taking n or m numbers at the time should work but: how long should it be initially? When should it regenerate? and so.

I hope I have explained clearly, thank you for your suggestions and contributions.

Hello I Van, I did what you advised me with a small change:

DynamicModule[{pc, n = 3, qc, m = 3, g, ct = 5},
 Column[{
   Row[{
     Column[{
       Slider[Dynamic[n], {1, 8, 1}, Appearance -> "Labeled"],
       Slider[Dynamic[m], {1, 8, 1}, Appearance -> "Labeled"]
       }],
     RadioButtonBar[
      Dynamic[ct], {5 -> \[DoubleStruckCapitalZ], 
       1 -> \[DoubleStruckCapitalQ]}]}
    ],
   pc = Dynamic[
     Function[g, Rationalize[g, ct*0.1]] /@ 
      RandomReal[{-10, 10}, n + 1]],
   qc = Dynamic[
     Function[g, Rationalize[g, ct*0.1]] /@ 
      RandomReal[{-10, 10}, m + 1]],
   Dynamic[Grid[{Sequence @@ pc, Sequence @@ qc}, Frame -> All]]
   }
  ]
 ]

As you noticed, I wrapped the Grid inside a Dynamic. However I still have a problem, the partial results and the final result do not match:

I guess it's due to the call to RandomReal. But I do not know how to make them match, any use of pc or qc will invoke RandomReal again. I appreciate your help

I move pc and qc into Dynamic, as you advise, it works well. But there is another related problem, I will try to explain with the code:

DynamicModule[{pc, n = 3, qc, m = 3, g, ct = 5},
 Column[{
   Row[{
     Column[{
       Slider[Dynamic[n], {1, 8, 1}, Appearance -> "Labeled"],
       Slider[Dynamic[m], {1, 8, 1}, Appearance -> "Labeled"]
       }],
     RadioButtonBar[
      Dynamic[ct], {5 -> Z], 
       1 -> Q]}]}
    ],
   Dynamic[
    pc = Function[g, Rationalize[g, ct*0.1]] /@ 
      RandomReal[{-10, 10}, n + 1]],
   Dynamic[
    qc = Function[g, Rationalize[g, ct*0.1]] /@ 
      RandomReal[{-10, 10}, m + 1]],
   Dynamic[Grid[{pc, qc}, Frame -> All]]
   }
  ]
 ]

If I run the above code, I get:

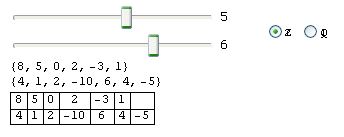
As expected, but I want to show, as a final result, only the grid. To hide the lists pc and qc I replace commas by semicolons where pc and qc are defined:

Dynamic[pc = 
  Function[g, Rationalize[g, ct*0.1]] /@ RandomReal[{-10, 10}, n + 1]];
Dynamic[qc = 
  Function[g, Rationalize[g, ct*0.1]] /@ RandomReal[{-10, 10}, m + 1]];
Dynamic[Grid[{pc, qc}, Frame -> All]]

But now the result is:

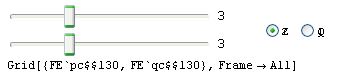
I have previously programmed with functional languages like Haskell but this one has me confused.

Your help is and will be appreciated.