Hey Radek,
That sounds awesome indeed, looking forward to seeing how it turns out!
Please see below and the attached files for the information you asked for and let me know if I can be of any more help.
I've attached a hierarchical dataset representation, here's how it looks like:
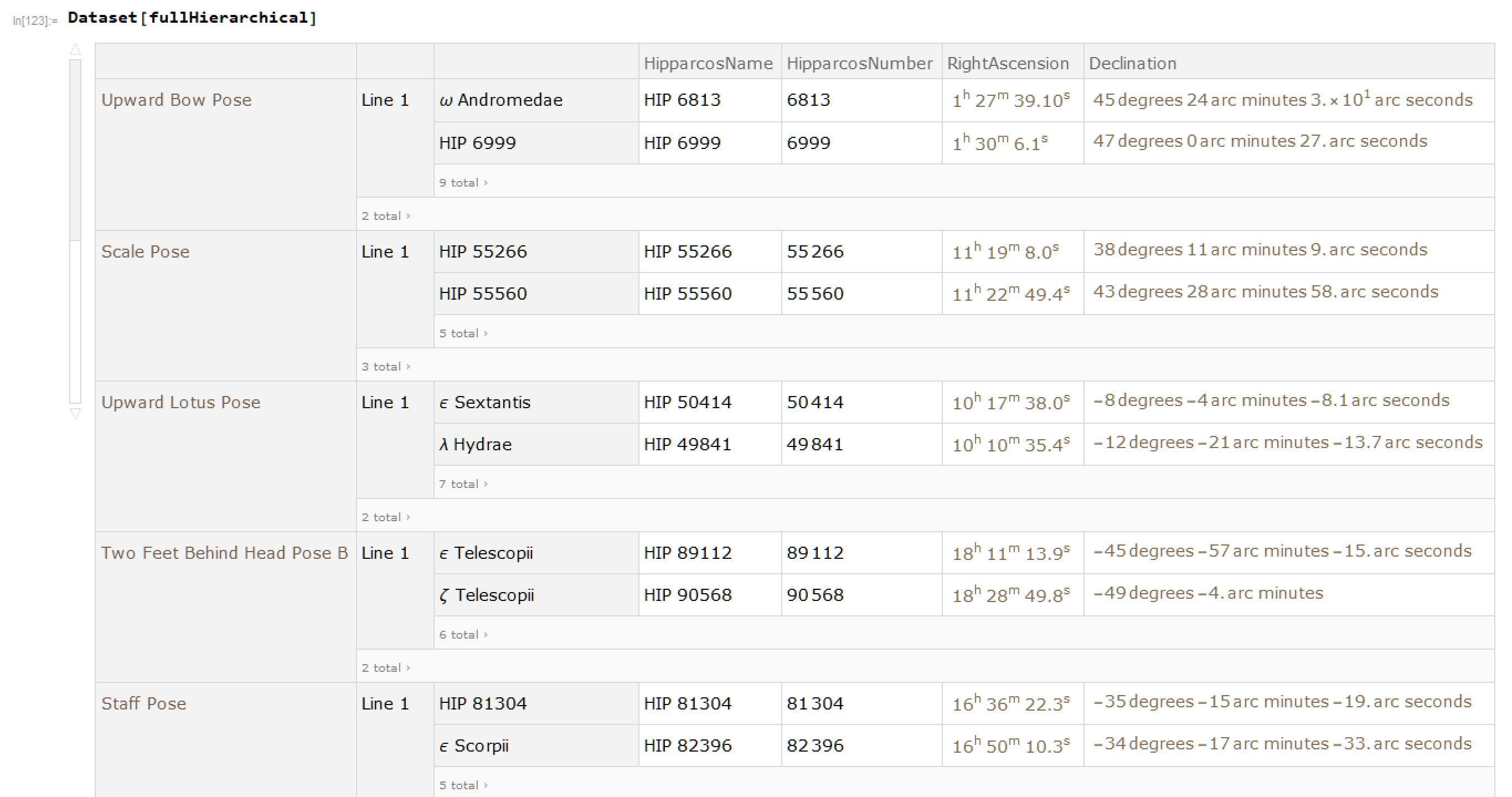
and a more detailed look for one of them:
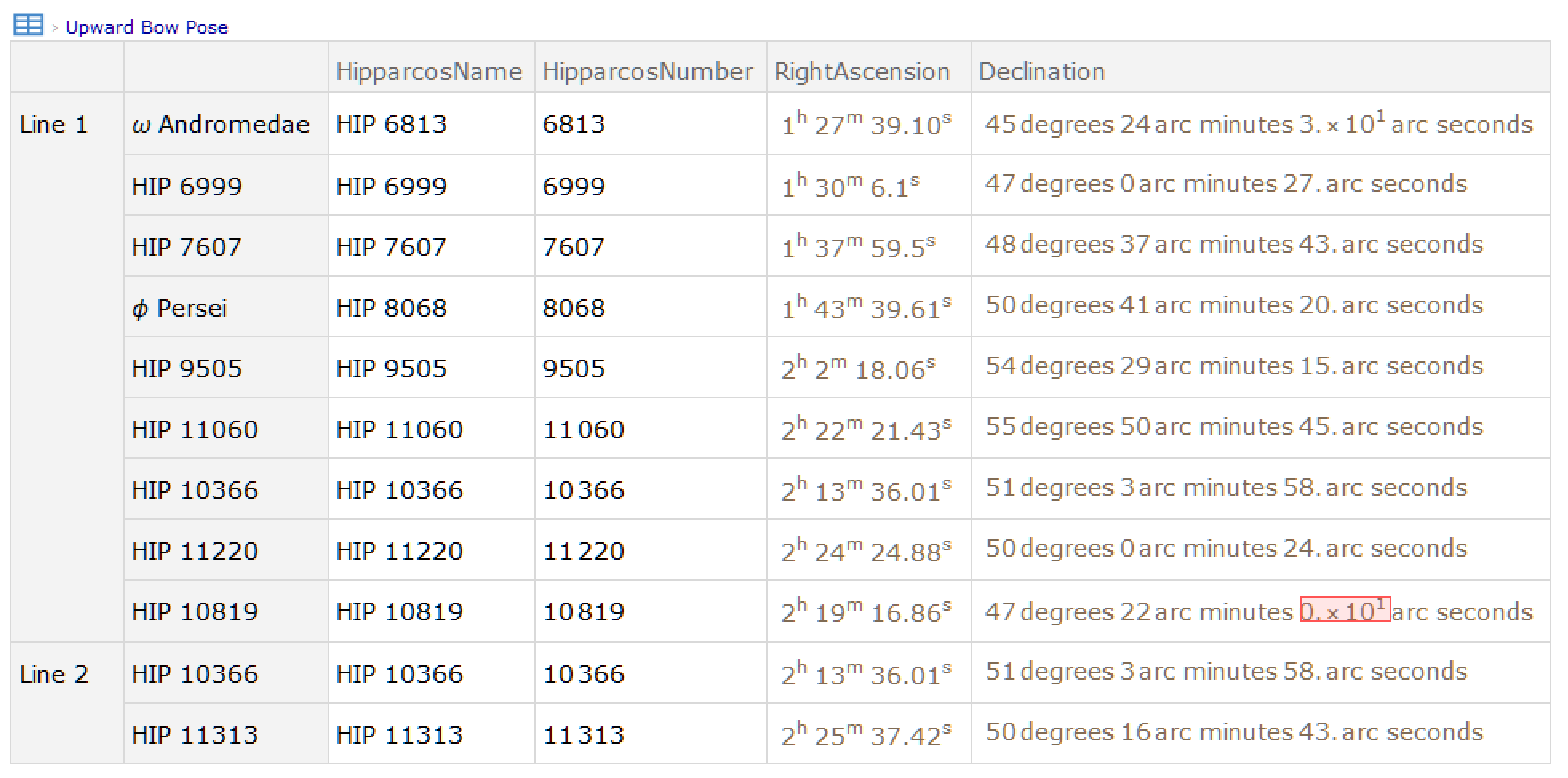
Note how they are grouped in lines (joining them in this order should give you the constellation shape).
Excited for this!
George
 Attachments:
Attachments: