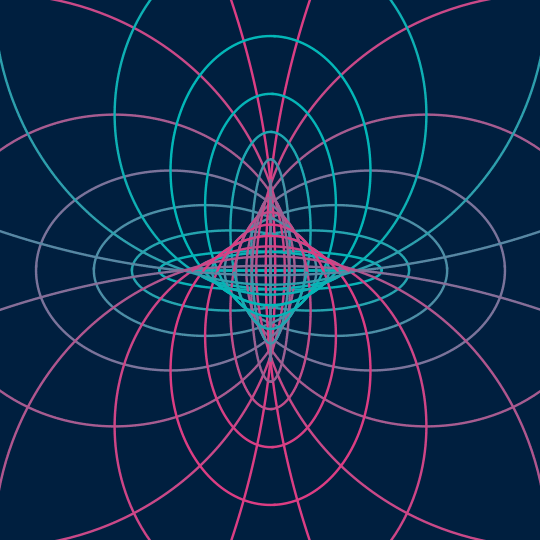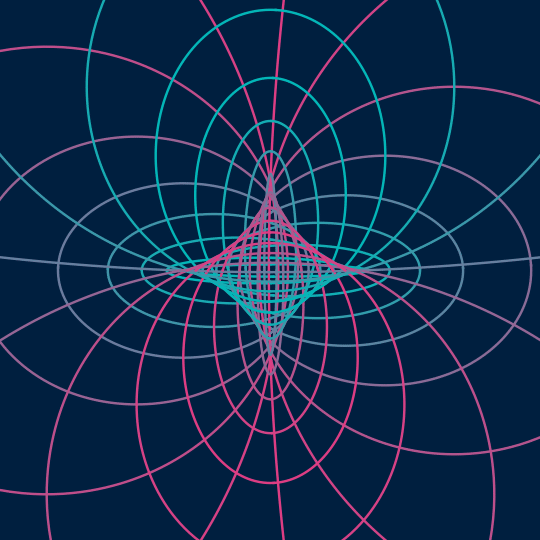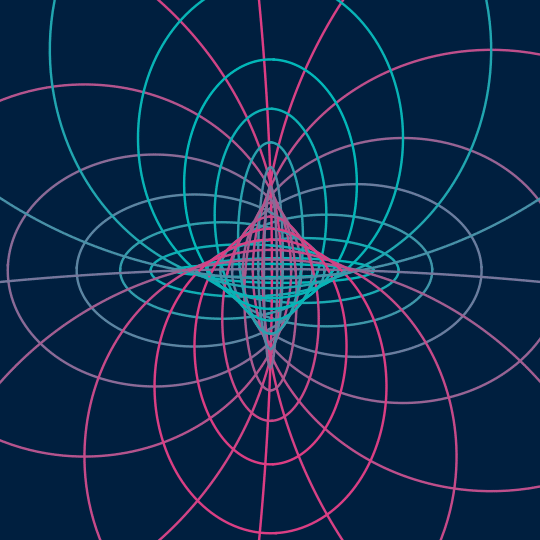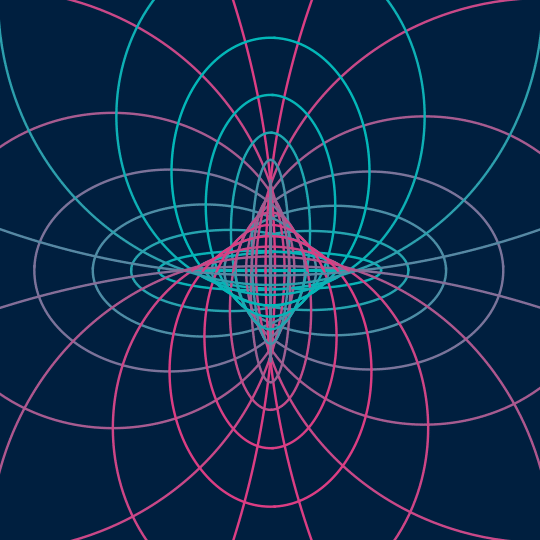
Flat
This is very much in the spirit of Send/Receive, but one dimension up. Now, I'm taking the surface $(\cos \theta \cos t, \cos \theta \sin t, \sin \theta \cos t, \sin \theta \sin t)$ inside the 3-sphere (which is just a flat torus, a rotated copy of the standard Clifford torus) as represented by the $\theta$- and $t$-coordinate grid lines, and stereographically projecting down to 3-space (actually, to produce the final animation, I'm then orthogonally projecting to the plane, which is what the [[;;2]] things are doing).
Here's the code:
Stereo[p_] := 1/(1 - p[[-1]]) p[[;; -2]]
With[{n = 15, cols = RGBColor /@ {"#de3d83", "#00b8b8", "#001F3F"}},
Manipulate[
Graphics[
{Thickness[.0045],
Table[
{Blend[cols[[;; 2]], 1/2 Cos[2 (\[Theta] + s)] + 1/2],
Line[
Table[
Stereo[{Cos[\[Theta] + s] Cos[t], Cos[\[Theta] + s] Sin[t], Sin[\[Theta] + s] Cos[t], Sin[\[Theta] + s] Sin[t]}][[2 ;;]],
{t, 0, \[Pi], \[Pi]/200}]]},
{\[Theta], 0, 2 \[Pi] - \[Pi]/n, \[Pi]/n}],
Table[
{Blend[cols[[;; 2]], 1/2 Sin[2 (t + s)] + 1/2],
Line[
Table[
Stereo[{Cos[\[Theta]] Cos[t + s], Cos[\[Theta]] Sin[t + s], Sin[\[Theta]] Cos[t + s], Sin[\[Theta]] Sin[t + s]}][[2 ;;]],
{\[Theta], 0, \[Pi], \[Pi]/200}]]},
{t, 0, 2 \[Pi] - \[Pi]/n, \[Pi]/n}]},
PlotRange -> 3, ImageSize -> 540, Background -> cols[[-1]]],
{s, 0, \[Pi]/n}]
]