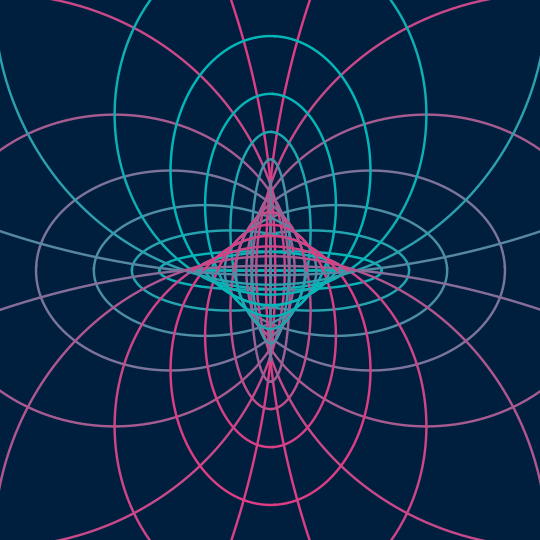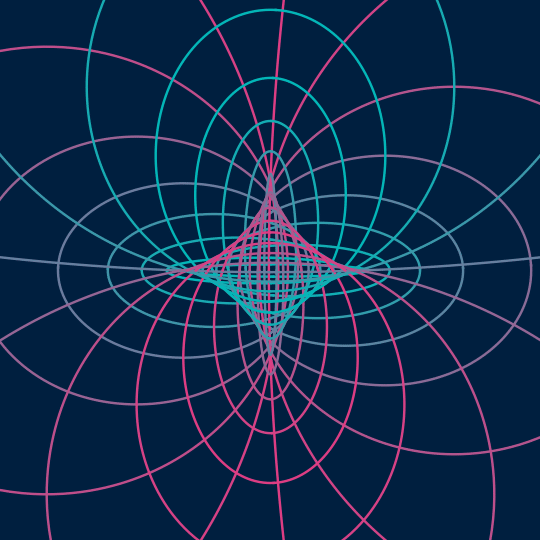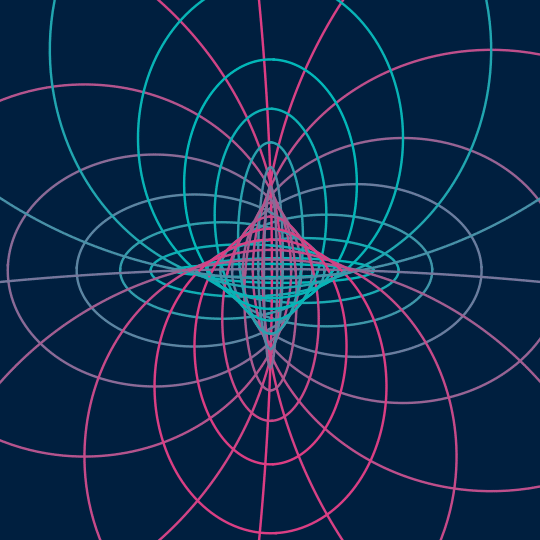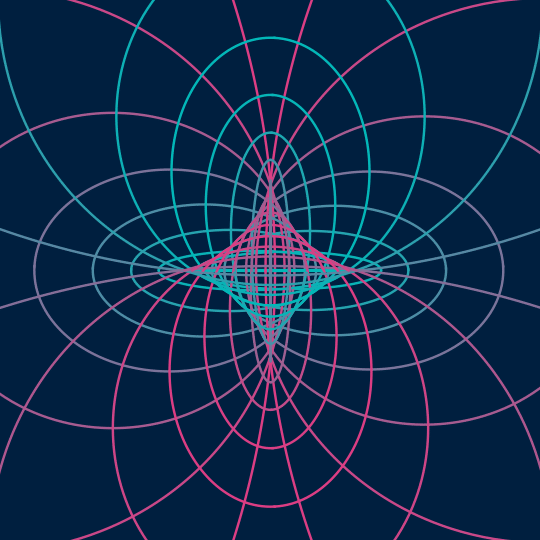
Flat

This is very much in the spirit of Send/Receive, but one dimension up. Now, I'm taking the surface $(\cos \theta \cos t, \cos \theta \sin t, \sin \theta \cos t, \sin \theta \sin t)$ inside the 3-sphere (which is just a flat torus, a rotated copy of the standard Clifford torus) as represented by the $\theta$- and $t$-coordinate grid lines, and stereographically projecting down to 3-space (actually, to produce the final animation, I'm then orthogonally projecting to the plane, which is what the [[;;2]] things are doing).

Here's the code:

Stereo[p_] := 1/(1 - p[[-1]]) p[[;; -2]]

With[{n = 15, cols = RGBColor /@ {"#de3d83", "#00b8b8", "#001F3F"}},
 Manipulate[
  Graphics[
   {Thickness[.0045],
    Table[
     {Blend[cols[[;; 2]], 1/2 Cos[2 (\[Theta] + s)] + 1/2],
      Line[
       Table[
        Stereo[{Cos[\[Theta] + s] Cos[t], Cos[\[Theta] + s] Sin[t], Sin[\[Theta] + s] Cos[t], Sin[\[Theta] + s] Sin[t]}][[2 ;;]],
        {t, 0, \[Pi], \[Pi]/200}]]},
     {\[Theta], 0, 2 \[Pi] - \[Pi]/n, \[Pi]/n}],
    Table[
     {Blend[cols[[;; 2]], 1/2 Sin[2 (t + s)] + 1/2],
      Line[
       Table[
        Stereo[{Cos[\[Theta]] Cos[t + s], Cos[\[Theta]] Sin[t + s], Sin[\[Theta]] Cos[t + s], Sin[\[Theta]] Sin[t + s]}][[2 ;;]],
        {\[Theta], 0, \[Pi], \[Pi]/200}]]},
     {t, 0, 2 \[Pi] - \[Pi]/n, \[Pi]/n}]},
   PlotRange -> 3, ImageSize -> 540, Background -> cols[[-1]]],
  {s, 0, \[Pi]/n}]
 ]