An Oloid is the convex hull of two circles in perpendicular planes, each going through the center of the other one.
Remove[schatzOloid]
schatzOloid[\[Delta]_Integer, \[Phi]_?NumericQ, \[Omega]_?NumericQ] :=
Block[{px =
Table[{0, Cos[o], Sin[o]}, {o, 0,
2 \[Pi] - \[Pi]/Mod[\[Delta], 100, 1],
N[\[Pi]/Mod[\[Delta], 100, 1]]}],
m1 = {{Cos[\[Phi]], 0, -Sin[\[Phi]]}, {0, 1, 0}, {Sin[\[Phi]], 0,
Cos[\[Phi]]}},
m2 = {{1, 0, 0}, {0, Cos[\[Omega]], -Sin[\[Omega]]}, {0,
Sin[\[Omega]], Cos[\[Omega]]}}, x},
x = Join[Plus[#, {0, 0, 1}] & /@ (Dot[m1, #] & /@ px),
Dot[m2, #] & /@ (Permute[#, {2, 1, 3}] & /@ px)
];
ConvexHullMesh[x,
PlotTheme -> "SmoothShading", Boxed -> True, Axes -> True,
AxesLabel -> {"X", "Y", "Z"}, Ticks -> None
] /; \[Delta] > 2
Use it to poke fun at ConvexHullMesh, so it works

this is an artefact, clearly (the Support is aware of it)

now apply the rotation matrices
(* 37 is freaky *)
Animate[schatzOloid[23, \[Phi], \[Omega]], {\[Phi],
0, \[Pi]}, {\[Omega], 0, \[Pi]}, AnimationRunning -> False]
]
and after a while you will see that
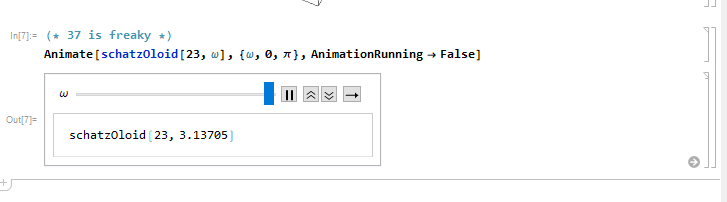
seemingly the definition got lost, Animate[] continues to print the name schatzOloid[] instead of calling what the name defined
or that
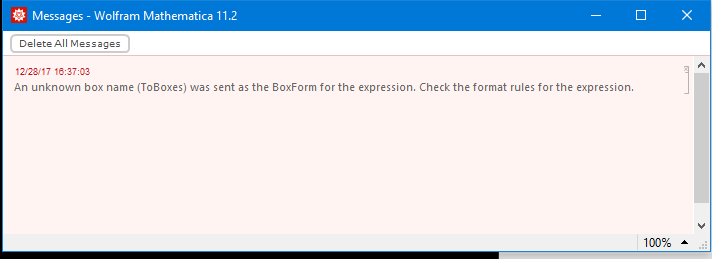
not so clear what is meant by this, because it runs under Mathematica 11.2.0.0 (Windows 10 Prof. (update 1709)) for minutes, before either the definition got lost or a formatting beep stopped the show.