Group Abstract Group Abstract

Message Boards Message Boards

Oloid under ConvexHullMesh

Udo Krause, NOrganization
Posted 8 years ago

An Oloid is the convex hull of two circles in perpendicular planes, each going through the center of the other one.

Remove[schatzOloid]
schatzOloid[\[Delta]_Integer, \[Phi]_?NumericQ, \[Omega]_?NumericQ] :=
  Block[{px = 
     Table[{0, Cos[o], Sin[o]}, {o, 0, 
       2 \[Pi] - \[Pi]/Mod[\[Delta], 100, 1], 
       N[\[Pi]/Mod[\[Delta], 100, 1]]}],
    m1 = {{Cos[\[Phi]], 0, -Sin[\[Phi]]}, {0, 1, 0}, {Sin[\[Phi]], 0, 
       Cos[\[Phi]]}},
    m2 = {{1, 0, 0}, {0, Cos[\[Omega]], -Sin[\[Omega]]}, {0, 
       Sin[\[Omega]], Cos[\[Omega]]}}, x},
   x = Join[Plus[#, {0, 0, 1}] & /@ (Dot[m1, #] & /@ px), 
     Dot[m2, #] & /@ (Permute[#, {2, 1, 3}] & /@ px)
     ];
   ConvexHullMesh[x,
    PlotTheme -> "SmoothShading", Boxed -> True, Axes -> True, 
    AxesLabel -> {"X", "Y", "Z"}, Ticks -> None
] /; \[Delta] > 2

Use it to poke fun at ConvexHullMesh, so it works

enter image description here

this is an artefact, clearly (the Support is aware of it)

enter image description here

now apply the rotation matrices

(* 37 is freaky *)
Animate[schatzOloid[23, \[Phi], \[Omega]], {\[Phi], 
  0, \[Pi]}, {\[Omega], 0, \[Pi]}, AnimationRunning -> False]
    ]

and after a while you will see that

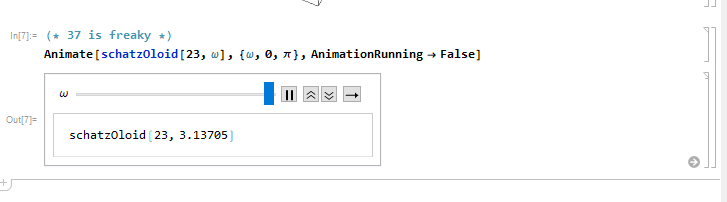
enter image description here

seemingly the definition got lost, Animate[] continues to print the name schatzOloid[] instead of calling what the name defined

or that

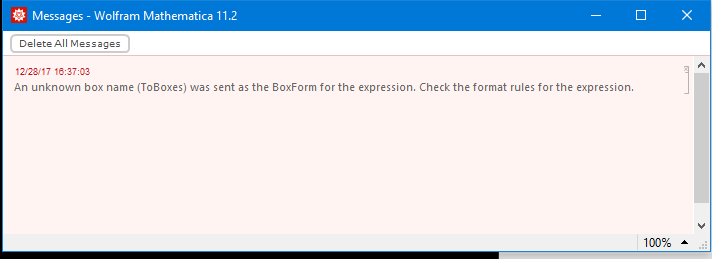
enter image description here

not so clear what is meant by this, because it runs under Mathematica 11.2.0.0 (Windows 10 Prof. (update 1709)) for minutes, before either the definition got lost or a formatting beep stopped the show.

POSTED BY: Udo Krause
5 Replies
Sort By:
Greg Hurst
Greg Hurst
Posted 8 years ago

FWIW, a workaround for the time being seems to be to translate the coordinates away from the y-axis before finding the convex hull:

schatzOloid[\[Delta]_Integer, \[Phi]_?NumericQ, \[Omega]_?NumericQ] :=
  Block[{px = 
     Table[{0, Cos[o], Sin[o]}, {o, 0, 
       2 \[Pi] - \[Pi]/Mod[\[Delta], 100, 1], 
       N[\[Pi]/Mod[\[Delta], 100, 1]]}],
    m1 = {{Cos[\[Phi]], 0, -Sin[\[Phi]]}, {0, 1, 0}, {Sin[\[Phi]], 0, 
       Cos[\[Phi]]}},
    m2 = {{1, 0, 0}, {0, Cos[\[Omega]], -Sin[\[Omega]]}, {0, 
       Sin[\[Omega]], Cos[\[Omega]]}}, x},
   x = Join[Plus[#, {0, 0, 1}] & /@ (Dot[m1, #] & /@ px), 
     Dot[m2, #] & /@ (Permute[#, {2, 1, 3}] & /@ px)
     ];
   res = TransformedRegion[ConvexHullMesh[{#1 + .1, ##2} & @@@ x], TranslationTransform[{-.1, 0, 0}]];
   BoundaryMeshRegion[res, PlotTheme -> "SmoothShading", Boxed -> True, 
    Axes -> True, AxesLabel -> {"X", "Y", "Z"}, Ticks -> None]
] /; \[Delta] > 2

schatzOloid[37, 0, 0]

enter image description here
POSTED BY: Greg Hurst

It is difficult to figure out what is belng claimed here (as ever, images of code do not equate to actual usable code). In[7] appears to use a form that was not defined (has only two arguments instead of the expected three). When I run the Animate that is given as actual code, it has no issue that I can see. That variant of course invokes schatzOloid with three arguments though.
POSTED BY: Daniel Lichtblau

I ran the following from the notebook.

Remove[schatzOloid0]
schatzOloid0[\[Delta]_Integer, \[Omega]_?NumericQ] := 
 Block[{px = 
     Table[{0, Cos[o], 1 + Sin[o]}, {o, 0, 
       2 \[Pi] - \[Pi]/Mod[\[Delta], 100, 1], 
       N[\[Pi]/Mod[\[Delta], 100, 1]]}],
    py = Table[{Cos[o], 0, Sin[o]}, {o, 0, 
       2 \[Pi] - \[Pi]/Mod[\[Delta], 100, 1], \[Pi]/
        Mod[\[Delta], 100, 1]}], 
    m = {{1, 0, 0}, {0, Cos[\[Omega]], -Sin[\[Omega]]}, {0, 
       Sin[\[Omega]], Cos[\[Omega]]}}, x},
   x = Join[px, Dot[m, #] & /@ py];
   ConvexHullMesh[x,
    PlotTheme -> "SmoothShading", Boxed -> True, Axes -> True, 
    AxesLabel -> {"X", "Y", "Z"}, Ticks -> None
    ]
   ] /; \[Delta] > 2

Animate[schatzOloid0[37, \[Omega]], {\[Omega], 0, \[Pi]}, 
 AnimationRunning -> False]

I then hit the play button and let it go for a couple of minutes. This is in version 11.2, running under Linux. I did not notice it stop and did not get an error message window. During this time I twice reevaluated the definition cell and also stopped/restarted the animation. Assuming I ran this as you expected, I do not know if it is platform dependent issue or if something else weird is going on (this remark is only with reference to the Animate issue, not the other one noted regarding parameters that are zero).
POSTED BY: Daniel Lichtblau

Okay, thank you; take your version as schatzOloid1; interestingly it runs under Animate (after the animation arrows have been clicked, of course (just for the logs))

Animate[schatzOloid1[23, \[Phi], \[Omega]], {\[Phi],   0, \[Pi]}, {\[Omega], 0, \[Pi]}, AnimationRunning -> False]

longer - for about 3 minutes - but then again Mathematica looses the definition.
POSTED BY: Udo Krause

schatzOloid is not an image of code, but anyway: find please in the appendix the notebook and the system Information about the machine to your comfort; Run the Animate commands each at least for a minute - just click the arrows and observe - with schatzOloid0 (2 Parameters, former schatzOloid) as well as with schatzOloid ( now 3 Parameters) - both loose seemingly the definition (in the original post the penultimate picture) and showing by chance the message about the beep, which is not in the notebook, but in the original post (last picture), because that's to my knowledge the only way to present it.

Attachments:
POSTED BY: Udo Krause
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard