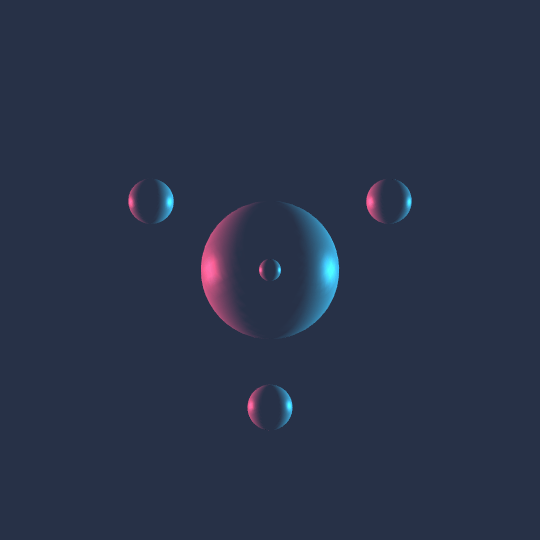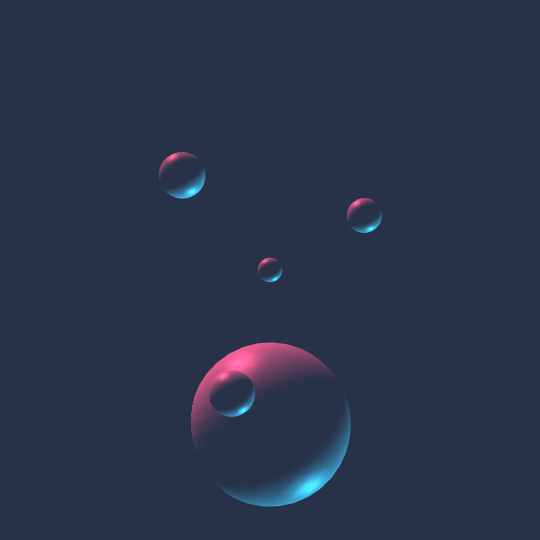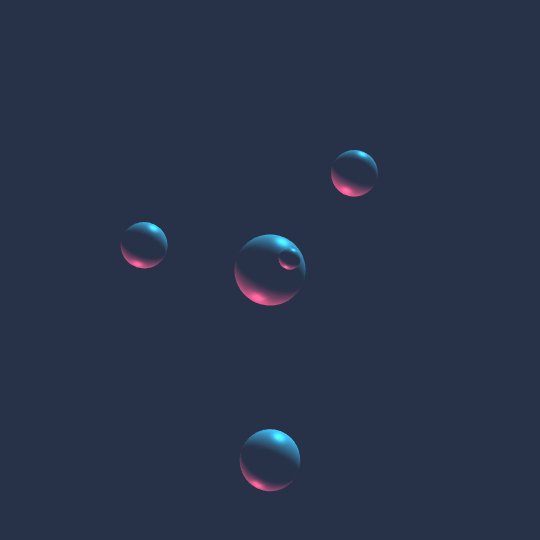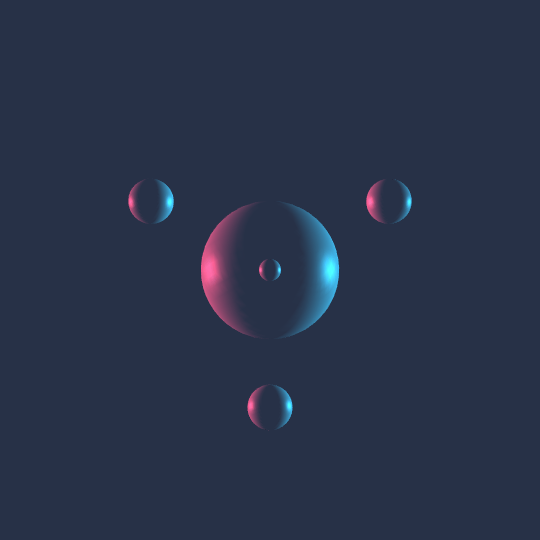
How Does That Work?

Very much the same idea as Touch ’Em All and All Day: think of the vertices of the 5-cell as living in the 3-sphere, put congruent spheres at each vertex, move them along a Hamiltonian cycle on the 1-skeleton of the 5-cell, then stereographically project the whole picture to $\mathbb{R}^3$.

I really like how this specific perspective creates a bit of a visual illusion.

Here's the code (once again leaving out the definition of ProjectedSphere[], which can be found here):

Stereo[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)}

smootheststep[t_] := -20 t^7 + 70 t^6 - 84 t^5 + 35 t^4;

fivecellvertices = 
  Normalize /@
   {{1/Sqrt[10], 1/Sqrt[6], 1/Sqrt[3], 1},
    {1/Sqrt[10], 1/Sqrt[6], 1/Sqrt[3], -1},
    {1/Sqrt[10], 1/Sqrt[6], -2/Sqrt[3], 0},
    {1/Sqrt[10], -Sqrt[3/2], 0, 0},
    {-2 Sqrt[2/5], 0, 0, 0}};

DynamicModule[
 {?, pts = N[fivecellvertices], angle, pts3d, v, b, 
  cols = RGBColor /@ {"#F23557", "#22B2DA", "#3B4A6B"}},
 angle = VectorAngle @@ pts[[;; 2]];
 pts3d = Stereo /@ pts;
 v = Normalize[pts3d[[2]] - pts3d[[1]]];
 b = Normalize[NullSpace[{v, pts3d[[-1]]}][[1]]];
 Manipulate[
  ? = smootheststep[1 - t];
  Graphics3D[
   {Specularity[.8, 50],
    Table[
     ProjectedSphere[RotationMatrix[angle*?, {pts[[i]], pts[[Mod[i + 1, Length[pts], 1]]]}].pts[[i]], .15],
     {i, 1, Length[pts]}]},
   Boxed -> False, PlotRange -> 3, ViewPoint -> v, 
   ViewVertical -> -pts3d[[-1]], ViewAngle -> ?/5, 
   Background -> Darker[cols[[-1]]], ImageSize -> 540, 
   Lighting -> {{"Directional", cols[[1]], RotationMatrix[2 ? ?, v].(b - v/2)},
     {"Directional", cols[[2]], -RotationMatrix[2 ? ?, v].(b + v/2)},
     {"Ambient", Darker[cols[[-1]]]}}],
  {t, 0, 1}]
 ]