
Loxo
This is very similar to the idea in Caught; here I'm generating a bunch of points on 10 different (congruent) loxodromes on the sphere, rotating the sphere, stereographically projecting the points to the plane, then forming the Voronoi cells of the resulting point set. The idea comes from Vincent Pantaloni's misinterpretation of what was going on in Caught; he thought I was using loxodromes, which I wasn't but seemed like a cool idea.
Anyway, to create the animation, first we need the stereographic projection function:
Stereo[p_] := p[[;; -2]]/(1 - p[[-1]])
Next, we need the points on 10 loxodromes:
pts = With[{n = 10},
Flatten[
Table[
1/Sqrt[1 + t^2] {Cos[t + ? + #], Sin[t + ? + #], -t} &[RandomVariate[NormalDistribution[0, .0001]]],
{?, 0., 2 ? - 2 ?/n, 2 ?/n}, {t, -60.,
60, .2}],
1]
];
The RandomVariate[] business is superfluous mathematically, but helps prevent VoronoiMesh[] from failing. Here's a visualization of those points on the sphere:
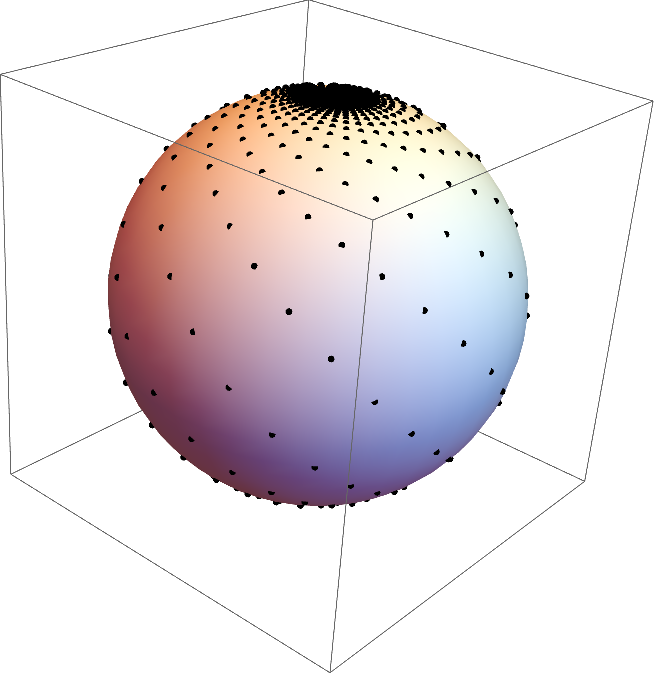
And then, finally, we can put the animation together:
With[{cols = RGBColor /@ {"#DA0463", "#283149"}},
Manipulate[
VoronoiMesh[
Stereo[RotationMatrix[?, {1., 0, 0}].#] & /@ pts,
{{-4.1, 4.1}, {-4.1, 4.1}},
PlotTheme -> "Lines", PlotRange -> 4, ImageSize -> 540, Background -> cols[[-1]],
MeshCellStyle -> {{1, All} -> Directive[Thickness[.005], cols[[1]]]}],
{?, 0, ?}
]
]