Yes, there seems to be a problem with the interpretation. But Wolfram|Alpha does in principle allow the underscore notation. If you use the second link on the OP for example you will see this:
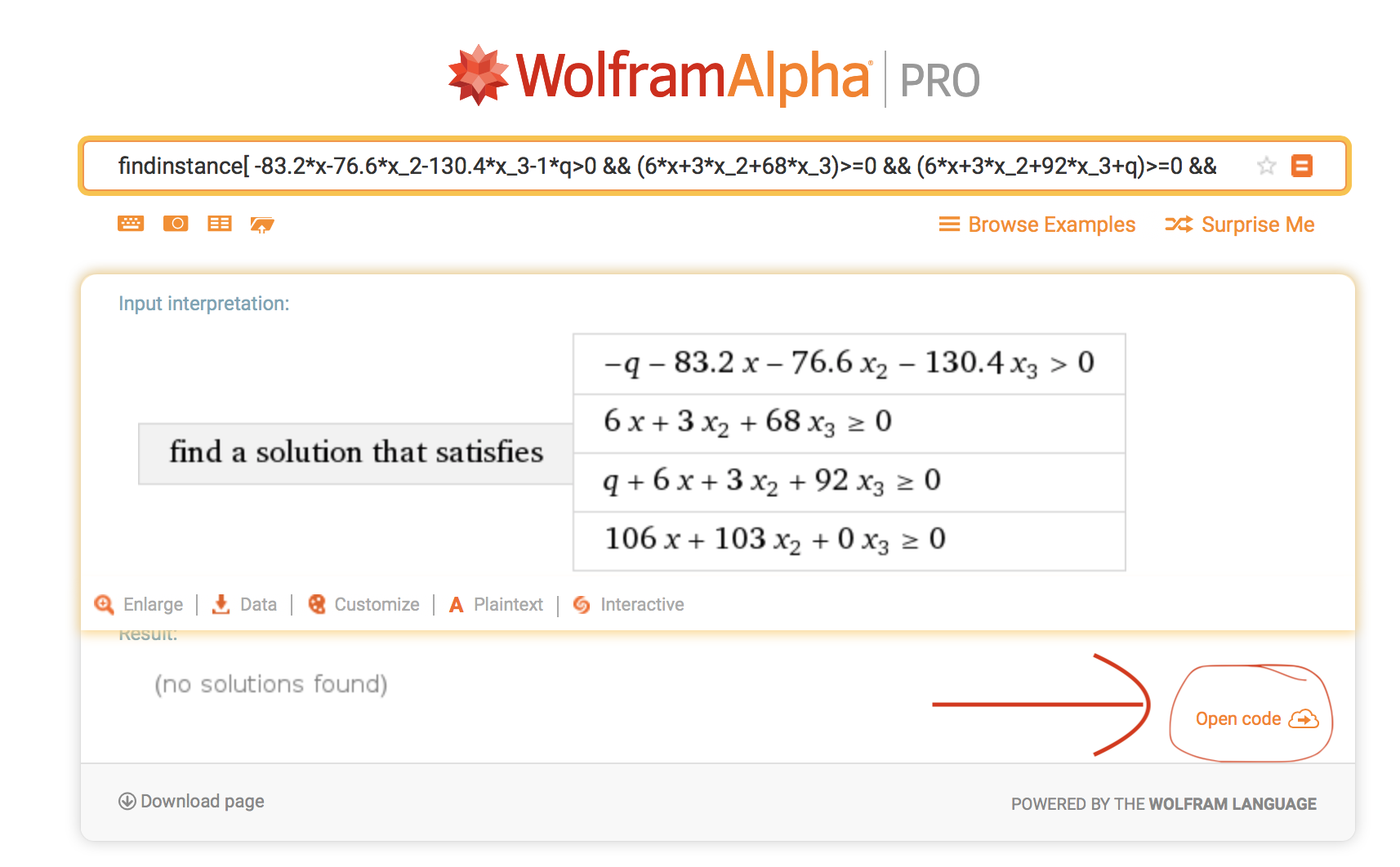
If you click on the open code icon, you will see how the input is interpreted. In the non-working example it is:

whereas in the working example it is:

So in principle the variable with underscores seem to be interpreted correctly, but for some reason the variable "x" is not used in the list variables to solve for, at least in the case of the non-working example. If all variables are consistently labelled with underscores it seems to work, and in both cases the additional "q" appears to be processed correctly.
If one adds the x manually to the list of variable to solve for, the problem disappears:
FindInstance[{-83.2 x - 76.6 Subscript[x, 2] - 130.4 Subscript[x, 3] - 1 q > 0, 6 x + 3 Subscript[x, 2] + 68 Subscript[x, 3] >= 0, 6 x + 3 Subscript[x, 2] + 92 Subscript[x, 3] + q >= 0, 106 x + 103 Subscript[x, 2] + 0 Subscript[x, 3] >= 0}, {q, x,Subscript[x, 2], Subscript[x, 3]}, Complexes]
(*{{q -> 5.45455 + 0. I, x -> 5.30606 + 0. I, Subscript[x, 2] -> -5.46061 + 0. I, Subscript[x, 3] -> -0.227273 + 0. I}}*)
So, I agree with the first reply that there is an issue with the underscores, the use of which should, in fact, be discouraged, but it seems to be a slightly more complex issue regarding the interpretation of the expression.
I don't think that the issue here in Wolfram|Alpha has anything to do with a misinterpretation in the form of pattern matching. Given that Wolfram|Alpha appears to interpret the underscored variables correctly and also identifies the q correctly, it is a bit unexpected that it would not treat the x accordingly, I think.
Best wishes,
Marco