I have a system of 3 non-linear ODEs of 2nd order with 3 unknown functions and 6 boundary conditions at Pi. I need to find functions numerically, get their plots and then calculate an integral containing these 3 functions. First is the system: I tried solving it with NDSolve but it gives me an error (NDSolve::ndsz: At x == 1.9672446444378016`, step size is effectively zero; singularity or stiff system suspected.) and the plots are wrong. I solved this system in Maple earlier so I think I'm making some syntax mistake since I'm not very familiar with Wolfram... Here's my code:
a = -10^2; b = 1; c = -2*10^(-3); m = 10^(-2); Rpi = 10^(-3); mupi = 4; Ypi = 10^(-2);
system = {R0''[x] + R0'[x]*Cot[x] == Exp[2*mu[x]]/2*((R0[x])^2 - c/a - m^2*(Y0[x])^2/a), R0[x]*Exp[2*mu[x]] == 2*(1 - mu''[x] - mu'[x]*Cot[x]), Y0''[x] + Y0'[x]*Cot[x] - m^2*Exp[2*mu[x]]*Y0[x] == 0, R0[Pi] == Rpi, R0'[Pi] == 0, mu[Pi] == mupi, mu'[Pi] == 0, Y0[Pi] == Ypi, Y0'[Pi] == 0}
sol = NDSolve[system, {R0, mu, Y0}, {x, 0, Pi}]
Plot[Evaluate[R0[x] /. sol], {x, 0, Pi}, PlotRange -> All]
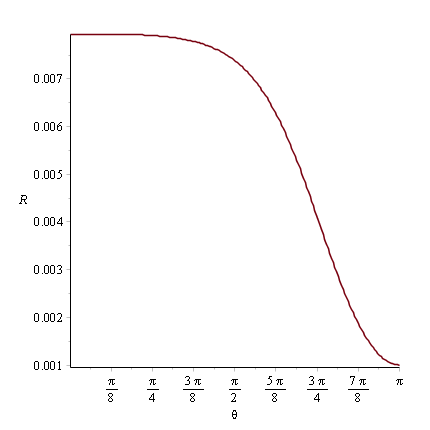
What am I doing wrong? I know that a cot(x) can create a singularuty, but only at 0 or Pi, not at 1.97... On Maple plots there are singularities at 0 and that's fine, but not in R(x):