TL;DR
I have three issues with getting sun positions in Mathematica V10:
- It is extremely slow compared to V9
- It doesn't seem to yield correct results
- a) It needs an Internet connection, which b) is not assured to always return results and c) if not used optimally can easily consume your monthly allowance of W|A calls
Long story
With the advent of V10 AstronomicalData has been deprecated, as shown on its documentation page:  .
.
I'm not an astronomer, so my main use of this function has been restricted to its capability to get the sun position using functions calls like this:
{
AstronomicalData["Sun", {"Azimuth", {2013, 3, 1, #, 0, 0}, {52.37`, 4.89`}}, TimeZone -> 1],
AstronomicalData["Sun", {"Altitude", {2013, 3, 1, #, 0, 0}, {52.37`, 4.89`}}, TimeZone -> 1]
} & /@ Range[0, 23]
{{341.47732, -43.93930}, {2.33417, -45.21747}, {22.94232, -43.19133}, {41.52167, -38.28400}, {57.55208, -31.30276}, {71.47253, -23.03159}, {84.02194, -14.08294}, {95.91940, -4.92723}, {107.80166, 4.03418}, {120.23770, 12.40167}, {133.72303, 19.72563}, {148.59433, 25.48377}, {164.84179, 29.12209}, {181.93103, 30.19428}, {198.91284, 28.55117}, {214.89602, 24.41962}, {229.46400, 18.28613}, {242.70064, 10.70703}, {254.98998, 2.19073}, {266.84760, -6.82566}, {278.85594, -15.94505}, {291.66723, -24.75464}, {306.00911, -32.75641}, {322.57956, -39.29877}}
So, this gets me the sun positions in steps of an hour during a particular day in Amsterdam (TZ 1).
The same call still works in V10, though it now returns numbers with units; degrees in this case. On its first call, it reads some paclet information from a Wolfram server, but on any successive call no Internet connection is needed. I will be going into detail about timing further on, but I'll say here that the V10 function takes about three times longer than its V9 namesake. I blame the addition of units for that.
With AstronomicalData apparently deprecated we are supposed to use its successors. In this case I need SunPosition. A direct translation of the above would be:
SunPosition[GeoPosition[{52.37`, 4.89`}], DateObject[{2013, 3, 1, #, 0, 0}, TimeZone -> 1]] & /@ Range[0, 23]
{{95.7, -5.1}, {107.6, 3.9}, {120.0, 12.3}, {133.5, 19.6}, {148.3, 25.4}, {164.5, 29.1}, {181.6, 30.2}, {198.6, 28.6}, {214.6, 24.5}, {229.2, 18.4}, {242.5, 10.9}, {254.8, 2.4}, {266.6, -6.7}, {278.6, -15.8}, {291.4, -24.6}, {305.7, -32.6}, {322.2, -39.2}, {341.3, -43.5}, {2.0, -44.8}, {22.5, -42.9}, {41.1, -38.0}, {57.1, -31.1}, {71.0, -22.9}, {83.6, -13.9}}
As with the new AstronomicalData the output is actually in degrees which I have removed in the above output for the sake of clarity. There are a few things to note:
SunPosition uses position and date objects, the latter being new in V10SunPosition does not have a TimeZone option, but you can set it in DateObjectSunPosition can use the old lat/long list position indication. It also can use a date list to enter the date instead of a DateObject. In the latter case you are out of options with respect to time zones and you have to add the appropriate amount of time offset- It is extremely slow, and it may even time-out:

- Last but not least: the results seem to be plain wrong. It suggests that sunrise is somewhat before 1 am, which is -of course- incorrect. I assume that this has something to do with a
$GeoLocation setting for the observer of the sun positions, but I haven't managed to sort out what I am supposed to enter to get the correct sun positions for the location provided in the same call.
As to timing: I noticed very inconsistent timings for SunPosition compared to AstronomicalData, so I used the following code to collect a somewhat more statistical sound sample:
SetAttributes[timingTest, HoldFirst];
timingTest[code_, repeats_Integer] :=
Table[
ClearSystemCache[];
code // AbsoluteTiming // First,
{repeats}
]
Using this, I collected timing of 20 calls to the following code snippets:
AstronomicalData V9 and V10: As aboveSunPosition: As aboveSunPosition without GeoPosition, just the lat/long list.SunPosition without GeoPosition, and also without the DateObject date, just a classical date list (with the hour set to +1 to accommodate TZ 1)SunPosition V10 without GeoPosition and with the Map (/@) gone and replaced by a DateRange inside the call.
In the last case, the returned value is a TimeSeries object from which I extract the positions using the "Paths" method:
SunPosition[{52.37`, 4.89`}, DateRange[{2013, 3, 1, 1, 0, 0}, {2013, 3, 1, 24, 0, 0}, "Hour"]]["Paths"][[1, All, 2]]
The results were as follows:
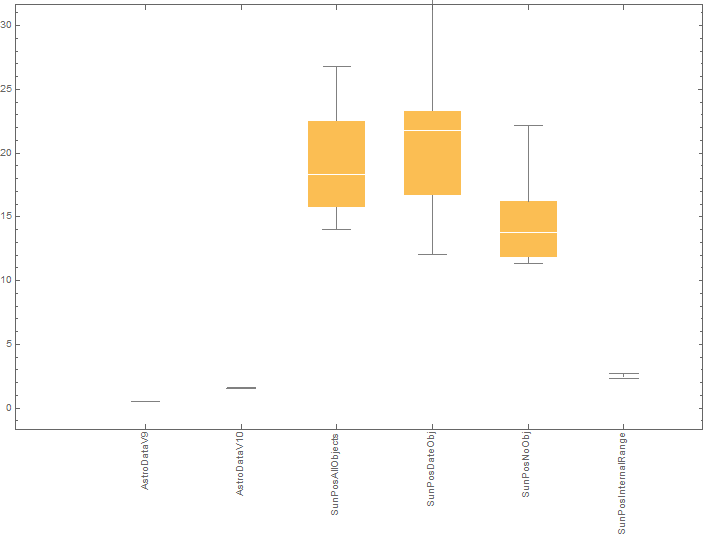
Clearly, the SunPosition results are very disappointing. Getting the sun positions with SunPosition is almost 40 times slower than using the old V9 method (which, I should add, wasn't particularly quick either. I have an implementation in Mathematica code which is faster). The V10 implementation of AstronomicalData is also more than three times slower than the V9 version. The DateRange version of the call saves a lot of communication overhead. Still, it is almost five times slower than in V9.
The cause of all this slowness is that SunPosition simply does a call to Wolfram|Alpha. Sniffing the communication one sees the following string passed to the server:
"1:eJxTTMoPSuNgYGAoZgESPpnFJcHcQEZwaV5AfnFmSWZ+XhoTsmxR/6GvGjH9wg4Qhr6XQxobsnzmXXYGhkxmIC+TEUSIgwggZihigIJgoAIGj/yizKr8PJigA5yBZtubwB1yrdxeDkXVIuvcH1aJOBRzAqUcS0vycxNLMpMBSAArww=="
which can be turned into readable form using Uncompress:
{"SunPosition", {4.89, 52.37}, {2013, 3, 1, 23, 0, 0.}, "Horizon", 2., 2., {52.09, 5.12}, Automatic}
Here, we can recognize the lat/long of the position I used (but with lat/long reversed - Is this somehow significant?). At the end is my own $GeoLocation, but I don't believe it is used at all (and it shouldn't: I'm asking for the sun position over Amsterdam, not where I live). Changing it with Block I get the same results:
Block[{$GeoLocation = GeoPosition[{52.37`, 40.89`}]}, SunPosition[{52.37`, 4.89`}, {2013, 3, 1, 1, 0, 0}]]
Apart from the slowness, there's the issue of the necessary Internet connectivity (Want to give a demonstration and you don't have Internet? Sorry, you're out of luck).
And what of the use of W|A calls? Each of the SunPosition tests (except the last one) took me 20 * 24 = 480 calls. So this part of my testing only already took 1440 calls, and one should be reminded that a typical Home Use license allows for only 3,000 calls per month. Things like this can go pretty fast. In fact, I once wrote an application that calculates the impact of building changes on shadows around your house throughout the year. It does in the order of 17,000 AstronomicalData calls. I couldn't implement that naively using SunPosition and have it actually work. Clearly, one should now use the DateRange version of the call as much as possible.
To wrap up: I have one real question, i.e., how to get SunPosition to return the same values as AstronomicalData, and a request to the WRI team: please put SunPosition in the kernel and don't use W|A calls, because the situation as it is now is rather annoying and IMHO a real step backwards.