UPDATED: More graphs added and some corrections.
A famous open problem is the Degree diameter problem. What is the largest regular graph with a given degree and diameter? Of the known solutions, we have two good pictures.
Grid[Transpose[{GraphData[#], #} & /@ {"PetersenGraph", "HoffmanSingletonGraph"}]]
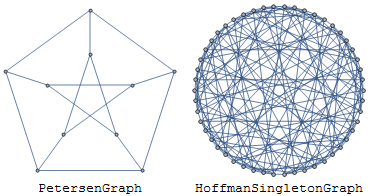
I found the Hoffman-Singleton embedding myself, and it's widely used now. But it's a challenge to find nice embeddings for highly-connected non-planar graphs. With Hoffman-Singleton I could confidently start with the assumption that some sort of symmetrical representation had to exist. Here are some edge lists for graphs we don't have good pictures for.
degreediameter33 = {{1, 2}, {1, 14}, {1, 20}, {2, 3}, {2, 8}, {3, 4}, {3, 18}, {4, 5}, {4, 11}, {5, 6}, {5, 15}, {6, 7}, {6, 19}, {7, 8}, {7, 12}, {8, 9}, {9, 10}, {9, 16}, {10, 11}, {10, 20}, {11, 12}, {12, 13}, {13, 14}, {13, 17}, {14, 15}, {15, 16}, {16, 17}, {17, 18}, {18, 19}, {19, 20}};
degreediameter34 = {{1,2},{1,36},{1,37},{2,3},{2,14},{3,4},{3,29},{4,5},{4,34},{5,6},{5,21},{6,7},{6,26},{7,8},{7,38},{8,9},{8,15},{9,10},{9,35},{10,11},{10,28},{11,12},{11,20},{12,13},{12,32},{13,14},{13,25},{14,15},{15,16},{16,17},{16,22},{17,18},{17,33},{18,19},{18,27},{19,20},{19,37},{20,21},{21,22},{22,23},{23,24},{23,30},{24,25},{24,36},{25,26},{26,27},{27,28},{28,29},{29,30},{30,31},{31,32},{31,38},{32,33},{33,34},{34,35},{35,36},{37,38}};
degreediameter35 = {{1,26},{1,41},{1,43},{2,30},{2,39},{2,44},{3,31},{3,34},{3,45},{4,23},{4,29},{4,46},{5,33},{5,42},{5,47},{6,34},{6,37},{6,48},{7,26},{7,32},{7,49},{8,24},{8,36},{8,50},{9,37},{9,40},{9,51},{10,29},{10,35},{10,52},{11,27},{11,39},{11,53},{12,22},{12,40},{12,54},{13,32},{13,38},{13,55},{14,30},{14,42},{14,56},{15,22},{15,25},{15,57},{16,35},{16,41},{16,58},{17,24},{17,33},{17,59},{18,25},{18,28},{18,60},{19,23},{19,38},{19,61},{20,27},{20,36},{20,62},{21,28},{21,31},{21,63},{22,43},{23,44},{24,45},{25,46},{26,47},{27,48},{28,49},{29,50},{30,51},{31,52},{32,53},{33,54},{34,55},{35,56},{36,57},{37,58},{38,59},{39,60},{40,61},{41,62},{42,63},{43,64},{44,64},{45,64},{46,65},{47,65},{48,65},{49,66},{50,66},{51,66},{52,67},{53,67},{54,67},{55,68},{56,68},{57,68},{58,69},{59,69},{60,69},{61,70},{62,70},{63,70}};
degreediameter42 = {{1,2},{1,4},{1,12},{1,13},{2,3},{2,8},{2,11},{3,4},{3,6},{3,15},{4,5},{4,10},{5,6},{5,8},{5,14},{6,7},{6,12},{7,8},{7,10},{7,13},{8,9},{9,10},{9,12},{9,15},{10,11},{11,12},{11,14},{13,14},{13,15},{14,15}};
degreediameter43 = {{1,2},{1,6},{1,26},{1,38},{2,3},{2,4},{2,5},{3,20},{3,24},{3,31},{4,13},{4,19},{4,25},{5,14},{5,18},{5,36},{6,7},{6,11},{6,35},{7,8},{7,9},{7,10},{8,25},{8,29},{8,39},{9,18},{9,24},{9,30},{10,19},{10,23},{10,31},{11,12},{11,16},{11,32},{12,13},{12,14},{12,15},{13,30},{13,34},{14,23},{14,29},{15,24},{15,28},{15,39},{16,17},{16,21},{16,38},{17,18},{17,19},{17,20},{18,33},{19,28},{20,29},{20,34},{21,22},{21,26},{21,35},{22,23},{22,24},{22,25},{23,37},{25,33},{26,27},{26,32},{27,28},{27,29},{27,30},{28,36},{30,37},{31,32},{31,41},{32,33},{33,40},{34,35},{34,41},{35,36},{36,40},{37,38},{37,41},{38,39},{39,40},{40,41}};
degreediameter44 = {{1,32},{1,50},{1,66},{1,92},{2,31},{2,49},{2,65},{2,91},{3,34},{3,52},{3,68},{3,94},{4,33},{4,51},{4,67},{4,93},{5,36},{5,54},{5,70},{5,96},{6,35},{6,53},{6,69},{6,95},{7,38},{7,56},{7,58},{7,98},{8,37},{8,55},{8,57},{8,97},{9,40},{9,44},{9,60},{9,86},{10,39},{10,43},{10,59},{10,85},{11,42},{11,46},{11,62},{11,88},{12,41},{12,45},{12,61},{12,87},{13,30},{13,48},{13,64},{13,90},{14,29},{14,47},{14,63},{14,89},{15,36},{15,64},{15,74},{15,95},{16,35},{16,63},{16,73},{16,96},{17,38},{17,66},{17,76},{17,97},{18,37},{18,65},{18,75},{18,98},{19,40},{19,68},{19,78},{19,85},{20,39},{20,67},{20,77},{20,86},{21,42},{21,70},{21,80},{21,87},{22,41},{22,69},{22,79},{22,88},{23,30},{23,58},{23,82},{23,89},{24,29},{24,57},{24,81},{24,90},{25,32},{25,60},{25,84},{25,91},{26,31},{26,59},{26,83},{26,92},{27,34},{27,62},{27,72},{27,93},{28,33},{28,61},{28,71},{28,94},{29,50},{29,79},{30,49},{30,80},{31,52},{31,81},{32,51},{32,82},{33,54},{33,83},{34,53},{34,84},{35,56},{35,71},{36,55},{36,72},{37,44},{37,73},{38,43},{38,74},{39,46},{39,75},{40,45},{40,76},{41,48},{41,77},{42,47},{42,78},{43,62},{43,90},{44,61},{44,89},{45,64},{45,92},{46,63},{46,91},{47,66},{47,94},{48,65},{48,93},{49,68},{49,96},{50,67},{50,95},{51,70},{51,98},{52,69},{52,97},{53,58},{53,86},{54,57},{54,85},{55,60},{55,88},{56,59},{56,87},{57,84},{58,83},{59,72},{60,71},{61,74},{62,73},{63,76},{64,75},{65,78},{66,77},{67,80},{68,79},{69,82},{70,81},{71,90},{72,89},{73,92},{74,91},{75,94},{76,93},{77,96},{78,95},{79,98},{80,97},{81,86},{82,85},{83,88},{84,87}};
degreediameter52 = {{1,4},{1,6},{1,7},{1,8},{1,9},{2,3},{2,5},{2,7},{2,8},{2,9},{3,6},{3,10},{3,11},{3,12},{4,5},{4,10},{4,11},{4,12},{5,13},{5,14},{5,15},{6,13},{6,14},{6,15},{7,16},{7,20},{7,23},{8,17},{8,21},{8,24},{9,18},{9,19},{9,22},{10,17},{10,19},{10,23},{11,18},{11,20},{11,24},{12,16},{12,21},{12,22},{13,17},{13,20},{13,22},{14,18},{14,21},{14,23},{15,16},{15,19},{15,24},{16,17},{16,18},{17,18},{19,20},{19,21},{20,21},{22,23},{22,24},{23,24}};
degreediameter62 = {{1,2},{1,3},{1,4},{1,19},{1,21},{1,30},{2,5},{2,6},{2,18},{2,24},{2,28},{3,7},{3,8},{3,20},{3,22},{3,29},{4,9},{4,10},{4,17},{4,23},{4,27},{5,10},{5,11},{5,14},{5,22},{5,26},{6,7},{6,12},{6,15},{6,25},{6,27},{7,13},{7,16},{7,23},{7,26},{8,9},{8,11},{8,14},{8,25},{8,28},{9,12},{9,15},{9,24},{9,26},{10,13},{10,16},{10,25},{10,29},{11,12},{11,20},{11,23},{11,30},{12,17},{12,21},{12,29},{13,14},{13,17},{13,24},{13,30},{14,18},{14,21},{14,27},{15,16},{15,18},{15,22},{15,30},{16,20},{16,21},{16,28},{17,19},{17,22},{17,28},{18,19},{18,23},{18,29},{19,20},{19,25},{19,26},{20,24},{20,27},{21,26},{21,31},{22,27},{22,31},{23,28},{23,31},{24,29},{24,31},{25,30},{25,31},{26,32},{27,32},{28,32},{29,32},{30,32},{31,32}};
degreediameter63 = {{1,39},{1,47},{1,53},{1,91},{1,106},{1,108},{2,40},{2,48},{2,54},{2,92},{2,107},{2,109},{3,41},{3,49},{3,55},{3,93},{3,108},{3,110},{4,42},{4,50},{4,56},{4,94},{4,109},{4,111},{5,43},{5,51},{5,57},{5,75},{5,95},{5,110},{6,44},{6,52},{6,58},{6,76},{6,96},{6,111},{7,45},{7,53},{7,59},{7,75},{7,77},{7,97},{8,46},{8,54},{8,60},{8,76},{8,78},{8,98},{9,47},{9,55},{9,61},{9,77},{9,79},{9,99},{10,48},{10,56},{10,62},{10,78},{10,80},{10,100},{11,49},{11,57},{11,63},{11,79},{11,81},{11,101},{12,50},{12,58},{12,64},{12,80},{12,82},{12,102},{13,51},{13,59},{13,65},{13,81},{13,83},{13,103},{14,52},{14,60},{14,66},{14,82},{14,84},{14,104},{15,53},{15,61},{15,67},{15,83},{15,85},{15,105},{16,54},{16,62},{16,68},{16,84},{16,86},{16,106},{17,55},{17,63},{17,69},{17,85},{17,87},{17,107},{18,56},{18,64},{18,70},{18,86},{18,88},{18,108},{19,57},{19,65},{19,71},{19,87},{19,89},{19,109},{20,58},{20,66},{20,72},{20,88},{20,90},{20,110},{21,59},{21,67},{21,73},{21,89},{21,91},{21,111},{22,60},{22,68},{22,74},{22,75},{22,90},{22,92},{23,38},{23,61},{23,69},{23,76},{23,91},{23,93},{24,39},{24,62},{24,70},{24,77},{24,92},{24,94},{25,40},{25,63},{25,71},{25,78},{25,93},{25,95},{26,41},{26,64},{26,72},{26,79},{26,94},{26,96},{27,42},{27,65},{27,73},{27,80},{27,95},{27,97},{28,43},{28,66},{28,74},{28,81},{28,96},{28,98},{29,38},{29,44},{29,67},{29,82},{29,97},{29,99},{30,39},{30,45},{30,68},{30,83},{30,98},{30,100},{31,40},{31,46},{31,69},{31,84},{31,99},{31,101},{32,41},{32,47},{32,70},{32,85},{32,100},{32,102},{33,42},{33,48},{33,71},{33,86},{33,101},{33,103},{34,43},{34,49},{34,72},{34,87},{34,102},{34,104},{35,44},{35,50},{35,73},{35,88},{35,103},{35,105},{36,45},{36,51},{36,74},{36,89},{36,104},{36,106},{37,38},{37,46},{37,52},{37,90},{37,105},{37,107},{38,79},{38,98},{38,103},{39,80},{39,99},{39,104},{40,81},{40,100},{40,105},{41,82},{41,101},{41,106},{42,83},{42,102},{42,107},{43,84},{43,103},{43,108},{44,85},{44,104},{44,109},{45,86},{45,105},{45,110},{46,87},{46,106},{46,111},{47,75},{47,88},{47,107},{48,76},{48,89},{48,108},{49,77},{49,90},{49,109},{50,78},{50,91},{50,110},{51,79},{51,92},{51,111},{52,75},{52,80},{52,93},{53,76},{53,81},{53,94},{54,77},{54,82},{54,95},{55,78},{55,83},{55,96},{56,79},{56,84},{56,97},{57,80},{57,85},{57,98},{58,81},{58,86},{58,99},{59,82},{59,87},{59,100},{60,83},{60,88},{60,101},{61,84},{61,89},{61,102},{62,85},{62,90},{62,103},{63,86},{63,91},{63,104},{64,87},{64,92},{64,105},{65,88},{65,93},{65,106},{66,89},{66,94},{66,107},{67,90},{67,95},{67,108},{68,91},{68,96},{68,109},{69,92},{69,97},{69,110},{70,93},{70,98},{70,111},{71,75},{71,94},{71,99},{72,76},{72,95},{72,100},{73,77},{73,96},{73,101},{74,78},{74,97},{74,102}};
degreediameter82 = {{1,9},{1,11},{1,17},{1,30},{1,36},{1,42},{1,48},{1,54},{2,3},{2,10},{2,17},{2,24},{2,31},{2,38},{2,45},{2,52},{3,10},{3,11},{3,12},{3,13},{3,14},{3,15},{3,16},{4,9},{4,10},{4,23},{4,29},{4,35},{4,41},{4,47},{4,53},{5,6},{5,10},{5,20},{5,30},{5,33},{5,43},{5,46},{5,56},{6,10},{6,19},{6,28},{6,37},{6,39},{6,48},{6,57},{7,8},{7,10},{7,22},{7,27},{7,32},{7,44},{7,49},{7,54},{8,10},{8,21},{8,25},{8,36},{8,40},{8,51},{8,55},{9,10},{9,18},{9,26},{9,34},{9,42},{9,50},{11,16},{11,23},{11,30},{11,37},{11,44},{11,51},{12,13},{12,20},{12,27},{12,34},{12,41},{12,48},{12,55},{13,19},{13,26},{13,33},{13,40},{13,47},{13,54},{14,15},{14,22},{14,29},{14,36},{14,43},{14,50},{14,57},{15,21},{15,28},{15,35},{15,42},{15,49},{15,56},{16,18},{16,25},{16,32},{16,39},{16,46},{16,53},{17,52},{17,53},{17,54},{17,55},{17,56},{17,57},{18,22},{18,28},{18,34},{18,40},{18,46},{18,52},{19,23},{19,26},{19,36},{19,39},{19,49},{19,52},{20,21},{20,30},{20,32},{20,41},{20,50},{20,52},{21,25},{21,37},{21,42},{21,47},{21,52},{22,29},{22,33},{22,44},{22,48},{22,52},{23,27},{23,35},{23,43},{23,51},{23,52},{24,31},{24,32},{24,33},{24,34},{24,35},{24,36},{24,37},{25,26},{25,31},{25,43},{25,48},{25,53},{26,31},{26,44},{26,50},{26,56},{27,31},{27,42},{27,46},{27,57},{28,31},{28,41},{28,51},{28,54},{29,30},{29,31},{29,39},{29,47},{29,55},{30,31},{30,40},{30,49},{32,35},{32,39},{32,50},{32,54},{33,42},{33,51},{33,53},{34,37},{34,43},{34,49},{34,55},{35,40},{35,48},{35,56},{36,41},{36,46},{37,44},{37,47},{37,57},{38,45},{38,46},{38,47},{38,48},{38,49},{38,50},{38,51},{39,42},{39,45},{39,55},{40,45},{40,57},{41,44},{41,45},{41,53},{42,45},{43,45},{43,54},{44,45},{44,56},{46,47},{46,56},{47,54},{49,53},{50,51},{50,57},{51,55},{53,57},{55,56}};
Here is what those graphs look like in an untamed state.
Can anyone find improved pictures for these graphs? The attached notebook has larger untamed degree-diameter graphs.
 Attachments:
Attachments: