How do I do it similarly for a ball hitting the floor at y=0?
You just need kinematics for this. May be something like this? (this was for a HW assignment, so code is not very clean. Did it in about 3 hrs). Most of the code deal with handling the state of the running simulation (reset, stop, step, etc...) if you do not care about all of this, you can remove all that and the code will shrink to 10% of its current size.
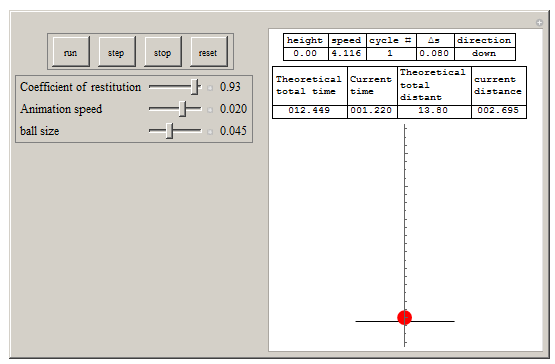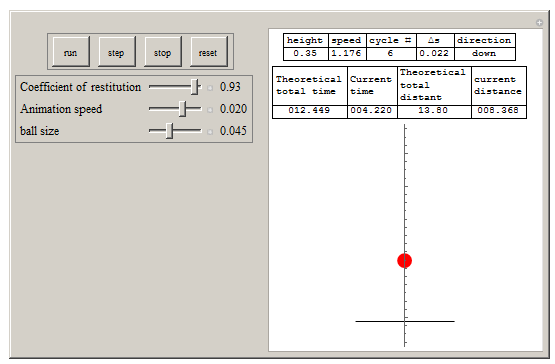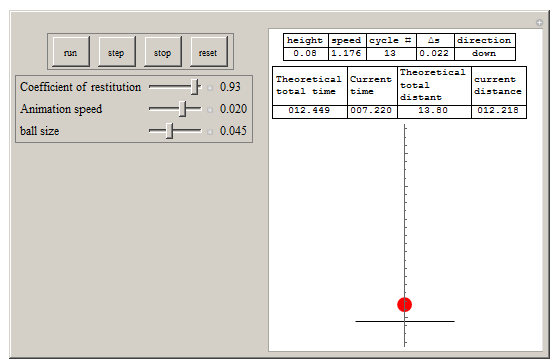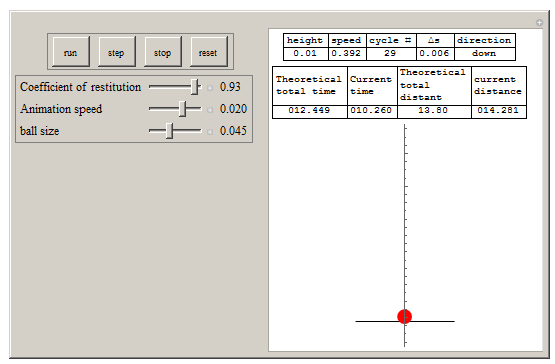
Manipulate[
tick;
h = 1;
g = 9.8;
If[(statex == "RUN" || statex == "STEP") && statex2 == "",
If[state == "down",
delS = currentV*delT + 1/2 g delT^2;
currentV += g *delT;
currentH -= delS
,
delS = currentV*delT - 1/2 g delT^2;
currentV -= g *delT;
currentH += delS
];
distantTravelled += delS
];
gr = Graphics[
{
Line[{{-.3, -r/2}, {.3, -r/2}}],
(*{LightGray,Dashed,Line[{{0,0},{0,1}}]},*)
{Red, Disk[{0, currentH}, r]}
},
PlotRange -> {{-.3, .3}, {-4 r, 1 + 4 r}}, Axes -> {False, True},
ImageSize -> {300, 300}];
gr = Grid[{
{Grid[{
{"height", "speed", "cycle #", "\[CapitalDelta]s", "direction"},
{padIt2[currentH, {3, 2}], padIt2[currentV, {4, 3}], padIt2[n, {1}],
padIt2[delS, {4, 3}], state}
}, Frame -> All]
},
{Grid[
{
{Column[{"Theoretical", "total time"}], Column[{"Current", "time"}],
Column[{"Theoretical", Column[{"total", "distant"}]}],
Column[{"current", "distance"}]},
{padIt2[tTime, {6, 3}], padIt2[currentT, {6, 3}],
padIt2[tDistance, {3, 2}], padIt2[totalDist, {6, 3}]
}
}, Frame -> All
]
},
{gr, SpanFromLeft}}];
If[statex2 == "pass",
statex2 = ""
,
currentT += delT;
totalDist += delS;
If[Abs@distantTravelled >= maxH,
distantTravelled = 0;
If[state == "down",
currentV = e*currentV;
state = "up";
n = n + 1;
maxH = e^(2*n)*h;
currentH = 0
,
state = "down";
currentV = 0;
currentH = maxH
]
]
];
If[statex == "RUN" && currentT < tTime,
tick = Not[tick]
];
gr,
{{tick, False}, None},
Text@Grid[{
{Grid[{
{Button[Text@Style["run", 12], {statex = "RUN"; tick = Not[tick]},
ImageSize -> {50, 40}],
Button[Text@Style["step", 12], {statex = "STEP"; tick = Not[tick]},
ImageSize -> {50, 40}],
Button[Text@Style["stop", 12], {statex = "STOP"; tick = Not[tick]},
ImageSize -> {50, 40}],
Button[
Text@Style["reset", 12], {statex = "STEP"; currentH = 1;
currentT = 0; n = 0;
distantTravelled = 0; currentV = 0; maxH = 1; state = "down";
totalDist = 0; statex2 = "";
tDistance = If[e == 1, Infinity, (1 + e^2)/(1 - e^2)];
tTime = If[e == 1, Infinity, Sqrt[2/9.81]*((1 + e)/(1 - e))];
tick = Not[tick]}, ImageSize -> {50, 40}]}
}, Frame -> True, FrameStyle -> Gray
], SpanFromLeft},
{Grid[{
{"Coefficient of restitution",
Manipulator[Dynamic[e, {e = #;
statex = "STEP";
currentH = 1;
currentT = 0; n = 0;
distantTravelled = 0;
currentV = 0;
maxH = 1;
state = "down";
totalDist = 0;
tDistance = If[e == 1, Infinity, (1 + e^2)/(1 - e^2)];
tTime = If[e == 1, Infinity, Sqrt[2/9.81]*((1 + e)/(1 - e))];
tick = Not[tick];
statex2 = "pass"} &], {0, 1, .01}, ImageSize -> Tiny],
Dynamic[padIt2[e, {2, 2}]],
SpanFromLeft},
{"Animation speed",
Manipulator[Dynamic[delT, {delT = #} &], {0.001, 0.03, 0.001},
ImageSize -> Tiny], Dynamic[padIt2[delT, {3, 3}]],
SpanFromLeft},
{"ball size",
Manipulator[
Dynamic[r, {r = #; tick = Not[tick], statex2 = "pass"} &], {0.01,
0.1, 0.001}, ImageSize -> Tiny], Dynamic[padIt2[r, {3, 3}]],
SpanFromLeft}
}, Alignment -> Left, Frame -> True, FrameStyle -> Gray]
}}],
{{n, 0}, None},
{{currentH, 1}, None},
{{currentT, 0}, None},
{{state, "down"}, None},
{{statex, "STEP"}, None},
{{statex2, ""}, None},
{{distantTravelled, 0}, None},
{{currentV, 0}, None},
{{maxH, 1}, None},
{{gr, 0}, None},
{{e, .9}, None},
{{delT, 0.02}, None},
{{r, 0.04}, None},
{{totalDist, 0}, None},
{{tDistance, (1 + (.9)^2)/(1 - (.9)^2)}, None},
{{tTime, Sqrt[2/9.81]*((1 + .9)/(1 - .9))}, None},
TrackedSymbols :> {tick},
Alignment -> Center,
SynchronousUpdating -> True,
SynchronousInitialization -> True,
FrameMargins -> 1,
ImageMargins -> 1,
ControlPlacement -> Left,
Initialization :>
{
padIt1[v_, f_List] :=
AccountingForm[Chop[v], f, NumberSigns -> {"-", "+"},
NumberPadding -> {"0", "0"}, SignPadding -> True];
padIt2[v_, f_List] :=
AccountingForm[Chop[v], f, NumberSigns -> {"", ""},
NumberPadding -> {"0", "0"}, SignPadding -> True]
}
]