Here is an animated GIF of a classical optimization problem: Regiomontanus' angle maximization problem. Below I give the Wolfram Language code that shows how to make it.
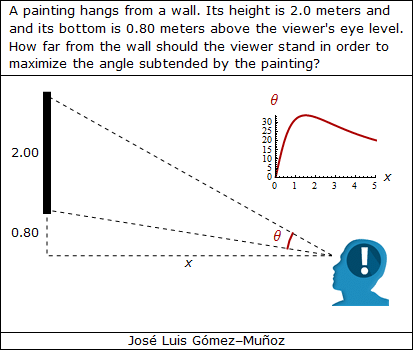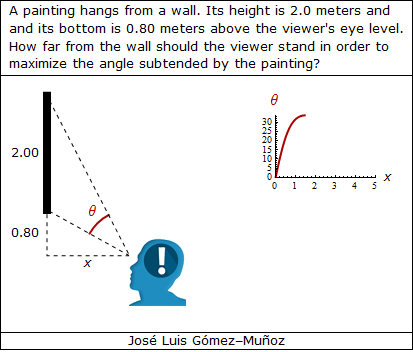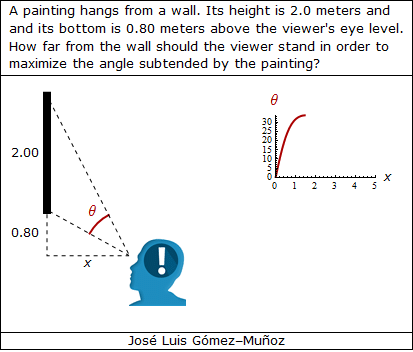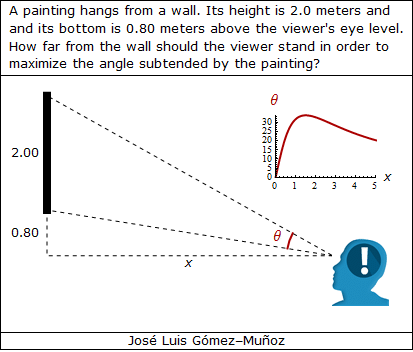
i = 0.80; a = 2.00; xini = 0.2; xmax = 5.0;
anima = Table[
distance = (xmax + xini)/2 + (xmax - xini)/2 Cos[2*Pi*t];
Column[{Column[{
Style[
"A painting hangs from a wall. Its height is 2.0 meters and",
FontFamily -> "Verdana"],
Style[
"and its bottom is 0.80 meters above the viewer's eye level.",
FontFamily -> "Verdana"],
Style[
"How far from the wall should the viewer stand in order to",
FontFamily -> "Verdana"],
Style["maximize the angle subtended by the painting?",
FontFamily -> "Verdana"]
}],
Graphics[{
GraphicsComplex[
{{distance, 0}, {0, 0}, {0, i}, {0, i + a},
{0, i + a/2}, {0, i/2}, {distance/2,
0}, {distance - 5 xini*Cos[ArcTan[(i + a/2)/distance]],
5 xini*Sin[ArcTan[(i + a/2)/distance]]}
},
{Darker[Red], Thick,
Circle[1,
4 xini, {\[Pi] - ArcTan[i/distance], \[Pi] -
ArcTan[(a + i)/distance]}],
Black, Thickness[0.02],
Line[{3, 4}],
Thin, Dashed,
Line[{1, 2, 3, 4, 1}],
Line[{1, 3}],
Text[
Style[NumberForm[a, {5, 2}], FontFamily -> "Verdana",
Larger], 5, {1.5, 0}],
Text[
Style[NumberForm[i, {5, 2}], FontFamily -> "Verdana",
Larger], 6, {1.5, 0}],
Text[Style[HoldForm[x], FontFamily -> "Verdana", Larger],
7, {0, 1}],
Text[
Style[HoldForm[\[Theta]], Darker[Red],
FontFamily -> "Verdana", FontSize -> 16], 8, {0, 0}]
}],
Inset["Insert image here", {distance, -1}, {0, -60}, 1],
Inset[
Plot[(ArcTan[(a + i)/x] - ArcTan[i/x])/Degree, {x, 0,
distance},
PlotRange -> {{0, xmax}, {0,
Module[{x},
NMaximize[{(ArcTan[(a + i)/x] - ArcTan[i/x])/Degree,
0 <= x <= xmax}, x][[1]]]}},
PlotStyle -> Directive[Darker[Red], Thick],
AxesLabel -> {Style[HoldForm[x], FontFamily -> "Verdana",
Larger],
Style[HoldForm[\[Theta]], Darker[Red],
FontFamily -> "Verdana", FontSize -> 16]}],
{-1 + xmax, i + a/3.5}, {0, 0}, 2.3]
}, PlotRange -> {{-0.7, 1.3 + xmax}, {-1.3, i + a + 0.3}},
ImageSize -> 400],
Style["José Luis Gómez-Muñoz", FontFamily -> "Verdana"]
}, Dividers -> All, Alignment -> {Center, Center}],
{t, 0, 1, 0.01}
];
name = "regiomon.gif";
Export[name, anima]