Here is an animated GIF of a classical optimization problem: Regiomontanus' angle maximization problem. Below I give the Wolfram Language code that shows how to make it.

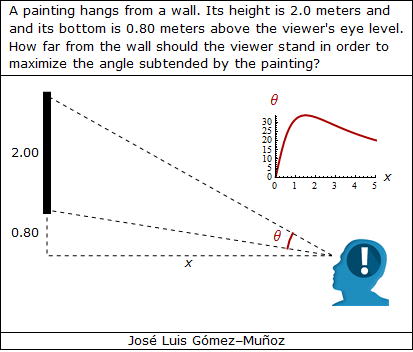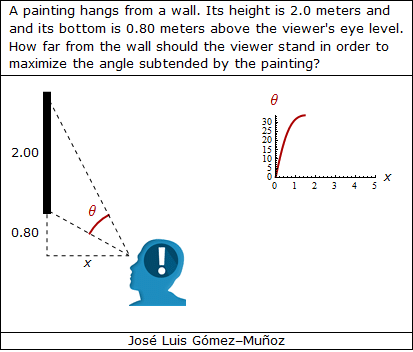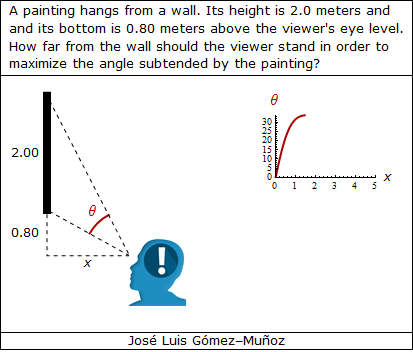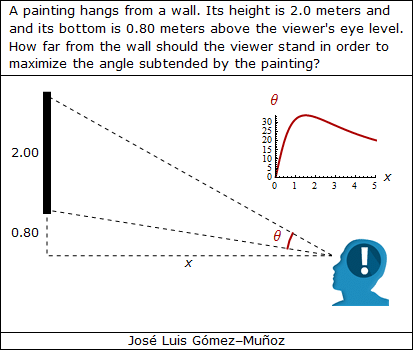
i = 0.80; a = 2.00; xini = 0.2; xmax = 5.0;
anima = Table[
   distance = (xmax + xini)/2 + (xmax - xini)/2 Cos[2*Pi*t];
   Column[{Column[{
       Style[
        "A painting hangs from a wall. Its height is 2.0 meters and", 
        FontFamily -> "Verdana"],
       Style[
        "and its bottom is 0.80 meters above the viewer's eye level.",
         FontFamily -> "Verdana"],
       Style[
        "How far from the wall should the viewer stand in order to", 
        FontFamily -> "Verdana"],
       Style["maximize the angle subtended by the painting?", 
        FontFamily -> "Verdana"]
       }],
     Graphics[{
       GraphicsComplex[
        {{distance, 0}, {0, 0}, {0, i}, {0, i + a},
         {0, i + a/2}, {0, i/2}, {distance/2, 
          0}, {distance - 5 xini*Cos[ArcTan[(i + a/2)/distance]], 
          5 xini*Sin[ArcTan[(i + a/2)/distance]]}
         },
        {Darker[Red], Thick,
         Circle[1, 
          4 xini, {\[Pi] - ArcTan[i/distance], \[Pi] - 
            ArcTan[(a + i)/distance]}],
         Black, Thickness[0.02],
         Line[{3, 4}],
         Thin, Dashed,
         Line[{1, 2, 3, 4, 1}],
         Line[{1, 3}],
         Text[
          Style[NumberForm[a, {5, 2}], FontFamily -> "Verdana", 
           Larger], 5, {1.5, 0}],
         Text[
          Style[NumberForm[i, {5, 2}], FontFamily -> "Verdana", 
           Larger], 6, {1.5, 0}],
         Text[Style[HoldForm[x], FontFamily -> "Verdana", Larger], 
          7, {0, 1}],
         Text[
          Style[HoldForm[\[Theta]], Darker[Red], 
           FontFamily -> "Verdana", FontSize -> 16], 8, {0, 0}]
         }],
       Inset["Insert image here", {distance, -1}, {0, -60}, 1],
       Inset[
        Plot[(ArcTan[(a + i)/x] - ArcTan[i/x])/Degree, {x, 0, 
          distance}, 
         PlotRange -> {{0, xmax}, {0, 
            Module[{x}, 
             NMaximize[{(ArcTan[(a + i)/x] - ArcTan[i/x])/Degree, 
                0 <= x <= xmax}, x][[1]]]}}, 
         PlotStyle -> Directive[Darker[Red], Thick], 
         AxesLabel -> {Style[HoldForm[x], FontFamily -> "Verdana", 
            Larger], 
           Style[HoldForm[\[Theta]], Darker[Red], 
            FontFamily -> "Verdana", FontSize -> 16]}],
        {-1 + xmax, i + a/3.5}, {0, 0}, 2.3]
       }, PlotRange -> {{-0.7, 1.3 + xmax}, {-1.3, i + a + 0.3}}, 
      ImageSize -> 400],
     Style["José Luis Gómez-Muñoz", FontFamily -> "Verdana"]
     }, Dividers -> All, Alignment -> {Center, Center}],
   {t, 0, 1, 0.01}
   ];
name = "regiomon.gif";
Export[name, anima]