Yesterday I posted a little piece of code to visualise the changing mean temperature of the earth. The animation tried to point out "how the temperature spirals out of control". In order to account for positive and negative deviations from the "standard" temperature, we needed to use a transformation from temperature difference to radius. This was non-linear and one might argue that lower temperatures are underrepresented.

Here is an alternative attempt.

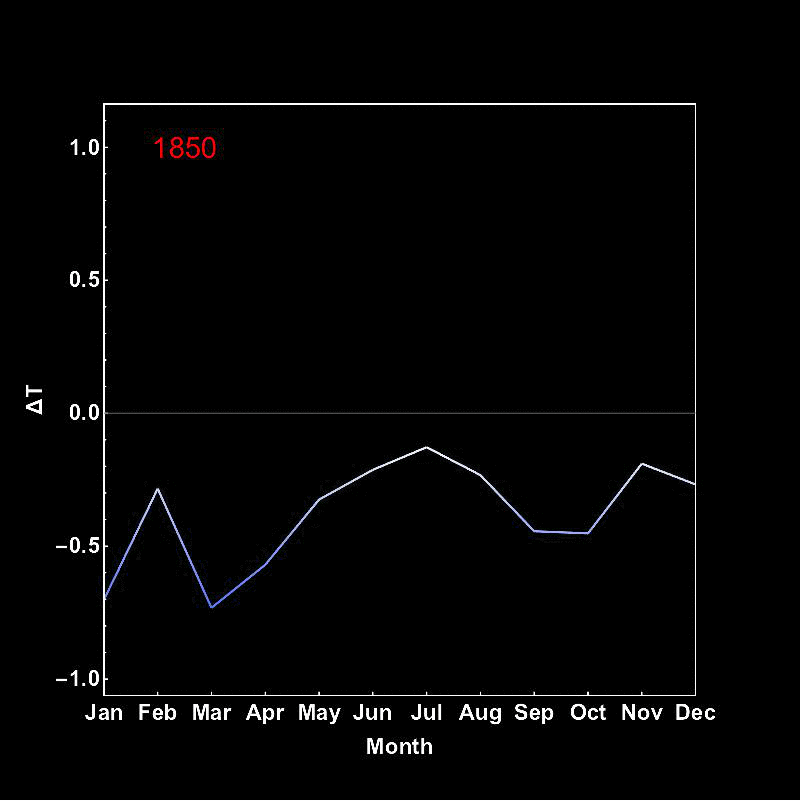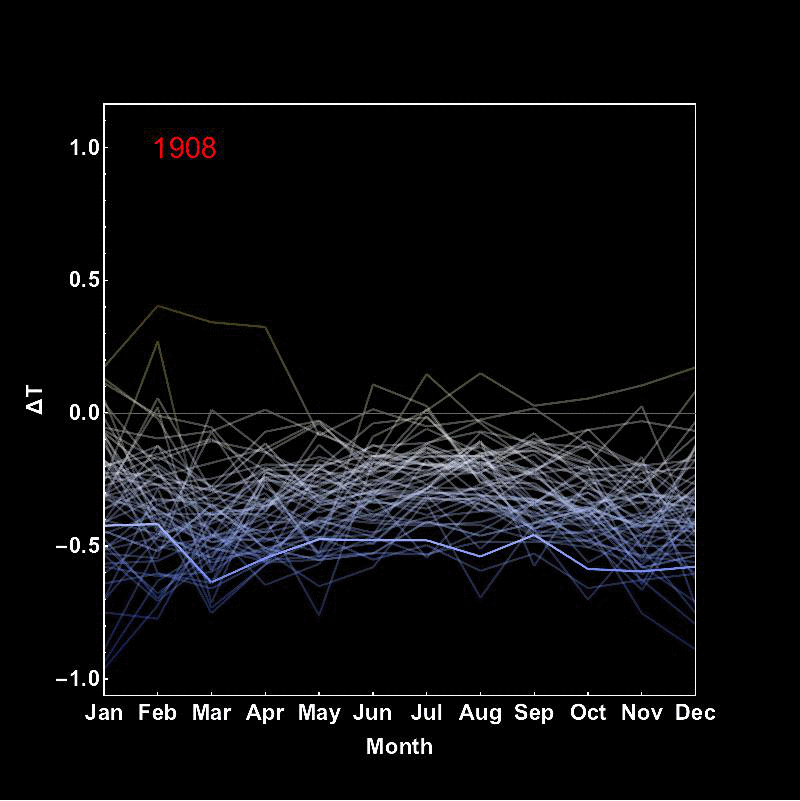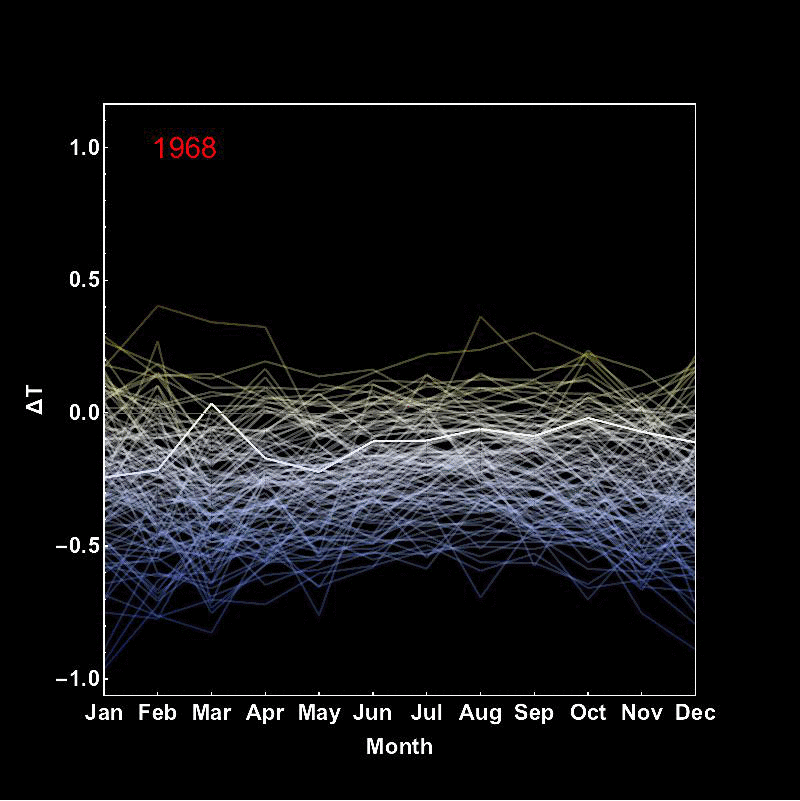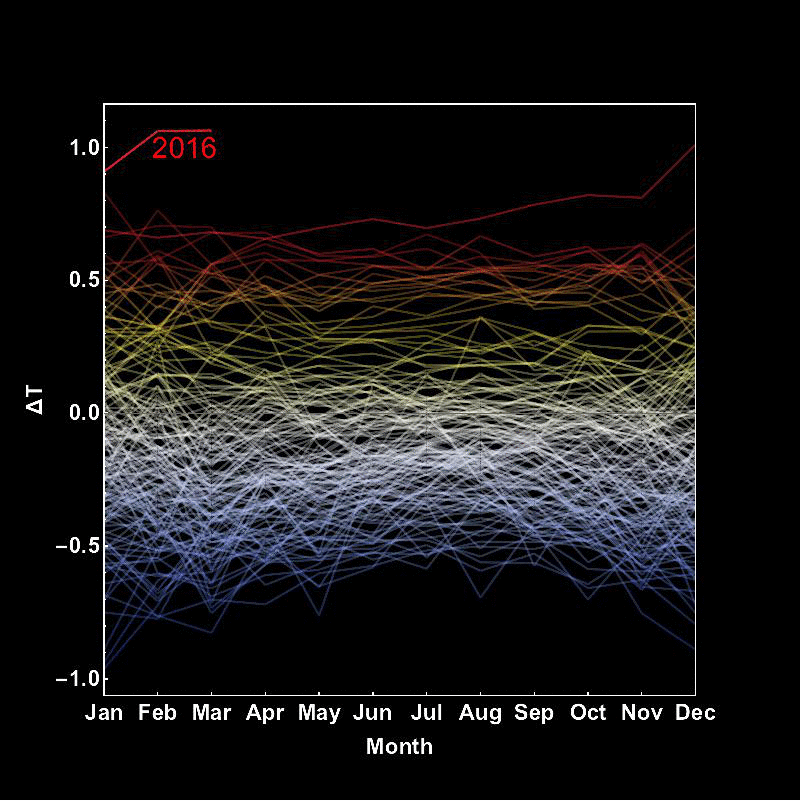
I do not post it in the same thread as the last post, because the gif is quite large and adding more the original thread might make it very slow to load. In spite of that I only have uploaded a lower quality video with every second frame. You can download the full quality file from here. Here's the implementation of the new idea, which I have seen in a similar fashion somewhere online:

tempdata = Transpose[{Interpreter["Date"][#[[All, 1]]], #[[All, 2]]}] &@ 
Import["http://www.metoffice.gov.uk/hadobs/hadcrut4/data/current/time_series/HadCRUT.4.4.0.0.monthly_ns_avg.txt", "Data"];
frames2 = 
Table[ListLinePlot[#, PlotStyle -> Table[Opacity[0.7/(1 + Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]] - j)^2 + 0.3], {j, 1, Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]]}], PlotRange -> {{1, 12}, Evaluate[MinMax[tempdata[[All, 2]]] + {-0.1, 0.1}]}, 
Frame -> True, Background -> Black, FrameStyle -> Directive[White, Bold, 16], LabelStyle -> Directive[White, Bold, 16], ImageSize -> Large, 
ColorFunction -> (ColorData["Temperature"][2^(#2) - 0.5] &), ColorFunctionScaling -> False, FrameTicks -> {{True, None}, {Transpose@{Range[12], {"Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"}}, None}}, FrameLabel -> {"Month", "\[CapitalDelta]T"}, 
ImagePadding -> 75, AspectRatio -> 1, Epilog -> {Text[Style[1849 + Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]], Red, 21], {2.5, 1.}]}] & @
Partition[tempdata[[All, 2]], UpTo[12]][[1 ;; Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]]]], {k, 1, Length[Partition[tempdata[[All, 2]], UpTo[12]]] + 10}];

You an list animate it:

ListAnimate[frames2]

I exported the frames:

Monitor[Do[Export["~/Desktop/ClimateGraph/frame" <> ToString[1000 + k] <> ".jpg", frames2[[k]], ImageResolution -> 100], {k, 1, Length[frames2], 1}], k]

and use the terminal command:

convert -delay 15 -loop 0 frame*.jpg animatedfull.gif

to create the animation above.

If you prefer the curves a bit smoother you can use:

frames3 = 
Table[ListLinePlot[#, PlotStyle -> Table[Opacity[0.7/(1 + Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]] - j)^2 + 0.3], {j, 1, Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]]}], PlotRange -> {{1, 12}, Evaluate[MinMax[tempdata[[All, 2]]] + {-0.1, 0.1}]}, InterpolationOrder->2,
Frame -> True, Background -> Black, FrameStyle -> Directive[White, Bold, 16], LabelStyle -> Directive[White, Bold, 16], ImageSize -> Large, 
ColorFunction -> (ColorData["Temperature"][2^(#2) - 0.5] &), ColorFunctionScaling -> False, FrameTicks -> {{True, None}, {Transpose@{Range[12], {"Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"}}, None}}, FrameLabel -> {"Month", "\[CapitalDelta]T"}, 
ImagePadding -> 75, AspectRatio -> 1, Epilog -> {Text[Style[1849 + Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]], Red, 21], {2.5, 1.}]}] & @
Partition[tempdata[[All, 2]], UpTo[12]][[1 ;; Min[k, Length[Partition[tempdata[[All, 2]], UpTo[12]]]]]], {k, 1, Length[Partition[tempdata[[All, 2]], UpTo[12]]] + 10}];

And proceed as before. The last frame looks like this:

Cheers,

Marco