Message Boards Message Boards

LinearProgramming approach for "best teams" algorithm

Anton Antonov, Accendo Data LLC
Posted 8 years ago

Here is the solution I outlined in my comments for this problem: Solve algorithm for best teams?

I do find the original formulation in the discussion opening inconsistent. The constraint formulations below are slightly different from the ones in OP's descriptions. The approach allows relatively easily the constraints to be changed or other constraints to be added.

The constraints and objective function were programmed in a way that allows the finding of the number groups for different number of teams and number of courses.

For another, detailed explanation of the used approach see this answer of the Mathematica Stackexchange question "How to fill a grid make its total be largest".

Original Formulation

The problem is about cooking. You need at least 18 people for it. Each group (2 people) are cooking either appetizer, main dish or dessert at their place. 2 other groups are visiting them. For the other two courses the group is the invited to another hosts' homes. Each location you meet new people (2 new groups). That means at the end you met 6 groups (12 people).

enter image description here

New Formulation

Variables

Number of variables

Assuming the number of groups is un-known we can select a large number for ng and then include the corresponding variables in the conditions and objective function.

Number of teams:

nt = 9;

Number of groups:

ng = 6;

Number of courses:

nc = 3;

Variable arrays

Clear[t, g, c, vt, vg, vc]

Binary variables telling that $i$-th team is going to be used (formed).

vt = Array[t, nt];

Binary variables telling that $i$-th group is going to be used (formed).

vg = Array[g, ng];

Binary variable for 

vc = Array[c, nc];

Teams in groups

Clear[ctg, vctg]

Each group has three teams. Each team is assigned to exactly one group per course.

Binary variables:

vctg = Flatten@Table[ctg[ci, ti, gi], {ci, nc}, {ti, nt}, {gi, ng}];
Length[vctg]
(* 162 *)

Chefs

Clear[ch, vch]

Each team can be the chef for a given group and course. There is only one chef per group and course pair.

Binary variable:

vch = Flatten@Table[ch[ci, ti, gi], {ci, nc}, {ti, nt}, {gi, ng}];
Length[vch]

(* 162 *)

Happiness

Happiness of team $t_i$ to prepare course $c_j$

Clear[H, vh]
vh = Flatten@Table[H[ci, ci], {ci, nc}, {ti, nt}];
Do[H[ci, ti] = RandomInteger[{0, 3}], {ci, nc}, {ti, nt}]

Constraints

Each team should have 3 courses

Each team should have 3 ( $nc$) courses. 

eachTeamHadFullMeal = 
  Flatten@Table[Sum[ctg[ci, ti, gi], {gi, ng}, {ci, nc}] == nc, {ti, nt}];
Length[eachTeamHadFullMeal]
(*eachTeamHadFullMeal[[1;;2]]*)

(* 9 *)

Each team is assigned to one group per course.

Each team is assigned to one group per course.

oneGroupPerTeamPerCourse = 
  Flatten@Table[
    Sum[ctg[ci, ti, gi], {gi, ng}] == 1, {ti, nt}, {ci, nc}];
Length[oneGroupPerTeamPerCourse]
oneGroupPerTeamPerCourse[[1 ;; 2]]

(* 27 *)

(* {ctg[1, 1, 1] + ctg[1, 1, 2] + ctg[1, 1, 3] + ctg[1, 1, 4] + 
ctg[1, 1, 5] + ctg[1, 1, 6] == 1, 
ctg[2, 1, 1] + ctg[2, 1, 2] + ctg[2, 1, 3] + ctg[2, 1, 4] + 
ctg[2, 1, 5] + ctg[2, 1, 6] == 1} *)

Each group has three teams.

Each group has three teams.

threeTeamsPerGroupPerCourse = 
  Flatten@Table[
    Sum[ctg[ci, ti, gi], {ti, nt}] - 3 g[gi] == 0, {gi, ng}, {ci, 
     nc}];
Length[threeTeamsPerGroupPerCourse]
threeTeamsPerGroupPerCourse[[1 ;; 2]]

(* 18 *)

(* {ctg[1, 1, 1] + ctg[1, 2, 1] + ctg[1, 3, 1] + ctg[1, 4, 1] + 
ctg[1, 5, 1] + ctg[1, 6, 1] + ctg[1, 7, 1] + ctg[1, 8, 1] + 
ctg[1, 9, 1] - 3 g[1] == 0, 
ctg[2, 1, 1] + ctg[2, 2, 1] + ctg[2, 3, 1] + ctg[2, 4, 1] + 
ctg[2, 5, 1] + ctg[2, 6, 1] + ctg[2, 7, 1] + ctg[2, 8, 1] + 
ctg[2, 9, 1] - 3 g[1] == 0} *)

There can be only one chef per group per course.

There can be only one chef per group per course. Not every team has to be a chef of a course.

oneChefPerGroupPerCourse = 
  Flatten@Table[
    Sum[ch[ci, ti, gi], {ti, nt}] - 1 g[gi] == 0, {gi, ng}, {ci, nc}];
Length[oneChefPerGroupPerCourse]
oneChefPerGroupPerCourse[[1 ;; 3]]

(* 18 *)

(* {ch[1, 1, 1] + ch[1, 2, 1] + ch[1, 3, 1] + ch[1, 4, 1] + ch[1, 5, 1] +
 ch[1, 6, 1] + ch[1, 7, 1] + ch[1, 8, 1] + ch[1, 9, 1] - g[1] == 0,
 ch[2, 1, 1] + ch[2, 2, 1] + ch[2, 3, 1] + ch[2, 4, 1] + 
 ch[2, 5, 1] + ch[2, 6, 1] + ch[2, 7, 1] + ch[2, 8, 1] + 
 ch[2, 9, 1] - g[1] == 0, 
 ch[3, 1, 1] + ch[3, 2, 1] + ch[3, 3, 1] + ch[3, 4, 1] + ch[3, 5, 1] +
 ch[3, 6, 1] + ch[3, 7, 1] + ch[3, 8, 1] + ch[3, 9, 1] - g[1] == 0} *)

Connect the $\text{ch}$ variables with $\text{ctg}$ variables.

connectChefTGAndCourseTG = 
  Flatten@Table[-ch[ci, ti, gi] + ctg[ci, ti, gi] >= 0, {ci, nc}, {ti,
      nt}, {gi, ng}];
Length[connectChefTGAndCourseTG]
connectChefTGAndCourseTG[[1 ;; 3]]

(* 162 *)

(* {-ch[1, 1, 1] + ctg[1, 1, 1] >= 0, -ch[1, 1, 2] + ctg[1, 1, 2] >= 0, -ch[1, 1, 3] + ctg[1, 1, 3] >= 0} *)

Set any team to be a chef only once.

Set any team to be a chef only once. (I think this means at most once given the previous constraint verbal formulation.)

anyTeamChefAtMostOnce = 
  Table[Sum[ch[ci, ti, gi], {gi, ng}, {ci, nc}] <= 1, {ti, nt}];
Length[anyTeamChefAtMostOnce]
anyTeamChefAtMostOnce[[1 ;; 2]]

(* 9 *)

(* {ch[1, 1, 1] + ch[1, 1, 2] + ch[1, 1, 3] + ch[1, 1, 4] + ch[1, 1, 5] +
ch[1, 1, 6] + ch[2, 1, 1] + ch[2, 1, 2] + ch[2, 1, 3] + 
ch[2, 1, 4] + ch[2, 1, 5] + ch[2, 1, 6] + ch[3, 1, 1] + 
ch[3, 1, 2] + ch[3, 1, 3] + ch[3, 1, 4] + ch[3, 1, 5] + 
ch[3, 1, 6] <= 1, 
ch[1, 2, 1] + ch[1, 2, 2] + ch[1, 2, 3] + ch[1, 2, 4] + ch[1, 2, 5] +
ch[1, 2, 6] + ch[2, 2, 1] + ch[2, 2, 2] + ch[2, 2, 3] + 
ch[2, 2, 4] + ch[2, 2, 5] + ch[2, 2, 6] + ch[3, 2, 1] + 
ch[3, 2, 2] + ch[3, 2, 3] + ch[3, 2, 4] + ch[3, 2, 5] + 
ch[3, 2, 6] <= 1} *)

Team in group cap, less than 4

teamInGroup = 
  Table[Sum[ctg[ci, ti, gi], {ci, nc}, {gi, ng}] <= 4, {ti, nt}];
Length[teamInGroup]
teamInGroup[[1 ;; 2]]

(* 9 *)

(* {ctg[1, 1, 1] + ctg[1, 1, 2] + ctg[1, 1, 3] + ctg[1, 1, 4] + 
 ctg[1, 1, 5] + ctg[1, 1, 6] + ctg[2, 1, 1] + ctg[2, 1, 2] + 
 ctg[2, 1, 3] + ctg[2, 1, 4] + ctg[2, 1, 5] + ctg[2, 1, 6] + 
 ctg[3, 1, 1] + ctg[3, 1, 2] + ctg[3, 1, 3] + ctg[3, 1, 4] + 
 ctg[3, 1, 5] + ctg[3, 1, 6] <= 4, 
 ctg[1, 2, 1] + ctg[1, 2, 2] + ctg[1, 2, 3] + ctg[1, 2, 4] + 
 ctg[1, 2, 5] + ctg[1, 2, 6] + ctg[2, 2, 1] + ctg[2, 2, 2] + 
 ctg[2, 2, 3] + ctg[2, 2, 4] + ctg[2, 2, 5] + ctg[2, 2, 6] + 
 ctg[3, 2, 1] + ctg[3, 2, 2] + ctg[3, 2, 3] + ctg[3, 2, 4] + 
 ctg[3, 2, 5] + ctg[3, 2, 6] <= 4} *)

All variables are binary

All variables are binary constraints. Needed if Maximize is used.

varConstraints = Map[0 <= # <= 1 &, Join[vctg, vch, vg]];
varConstraints[[1 ;; 4]]

(* {0 <= ctg[1, 1, 1] <= 1, 0 <= ctg[1, 1, 2] <= 1, 
  0 <= ctg[1, 1, 3] <= 1, 0 <= ctg[1, 1, 4] <= 1} *)

Objective function

objFunc =
  Sum[H[ci, ti] ch[ci, ti, gi], {ti, nt}, {ci, nc}, {gi, ng}];

We can use this objective function in order to minimize the number of groups:

objFuncMinNG = 
  Sum[H[ci, ti] ch[ci, ti, gi], {ti, nt}, {ci, nc}, {gi, ng}] - Total[vg];

Solving with LinearProgramming

Using Maximize is very slow, so we have to convert the conditions into matrix-vector formulation to be given to LinearProgramming.

All variables

vars = Join[vctg, vch, vg];
Length[vars]

(* 330 *)

Convert conditions to matrices

{zeroMat, mat0} = CoefficientArrays[eachTeamHadFullMeal[[All, 1]], vars];
Dimensions[mat0]

{zeroMat, mat1} = 
  CoefficientArrays[oneGroupPerTeamPerCourse[[All, 1]], vars];
Dimensions[mat1]

{zeroMat, mat2} = 
  CoefficientArrays[threeTeamsPerGroupPerCourse[[All, 1]], vars];
Dimensions[mat2]

{zeroMat, mat3} = 
  CoefficientArrays[oneChefPerGroupPerCourse[[All, 1]], vars];
Dimensions[mat3]

{zeroMat, mat4} = 
  CoefficientArrays[connectChefTGAndCourseTG[[All, 1]], vars];
Dimensions[mat4]

{zeroMat, mat5} = 
  CoefficientArrays[anyTeamChefAtMostOnce[[All, 1]], vars];
Dimensions[mat5]

{zeroMat, mat6} = CoefficientArrays[teamInGroup[[All, 1]], vars];
Dimensions[mat6]

bVec =
  Join[
   Table[{nc, 0}, {Dimensions[mat0][[1]]}],
   Table[{1, 0}, {Dimensions[mat1][[1]]}],
   Table[{0, 0}, {Dimensions[mat2][[1]]}],
   Table[{0, 0}, {Dimensions[mat3][[1]]}],
   Table[{0, 1}, {Dimensions[mat4][[1]]}],
   Table[{1, -1}, {Dimensions[mat5][[1]]}],
   Table[{4, -1}, {Dimensions[mat6][[1]]}]
   ];
Length[bVec]

condMat = Join[mat0, mat1, mat2, mat3, mat4, mat5, mat6];
MatrixQ[condMat]

MatrixPlot[condMat]

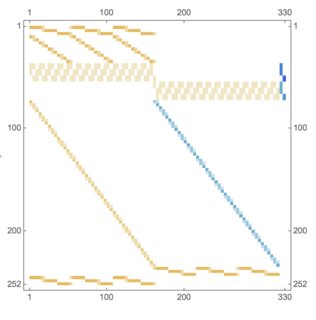
enter image description here

objVec = Normal@CoefficientArrays[{objFunc}, vars][[2]][[1]];
Length[objVec]
(* 330 *)

Solving

AbsoluteTiming[
 nsol = LinearProgramming[-objVec, condMat, bVec, 
    Table[{0, 1}, {Length[vars]}], Integers];
 ]
(* {0.063444, Null} *)

objVec.nsol
(* 23 *)

sol = Thread[vars -> nsol];

Tabulate solution

Find non-zero groups

gnzInds = 
  Table[Sum[ctg[ci, ti, gi], {ci, nc}, {ti, nt}] > 0, {gi, ng}] /. sol;
gnzInds = Pick[Range[ng], gnzInds]

Tabulation per group

This package is for the function CrossTabulate.

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MathematicaForPredictionUtilities.m"]

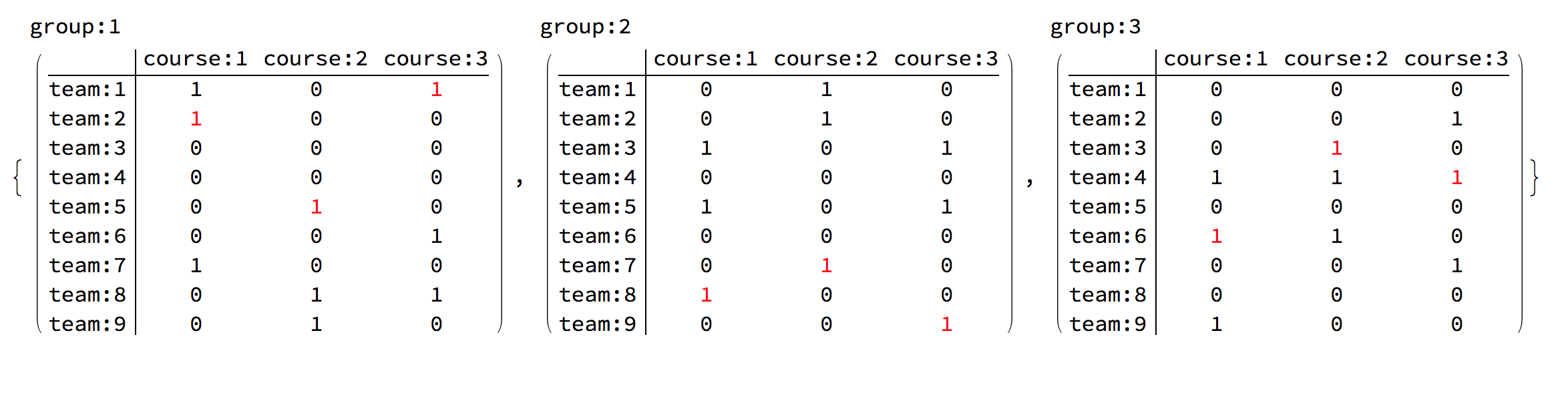
In red are the chef team assigments.

Table[
 Column[{Row[{"group:", gi}], 
   mf = MatrixForm[
     CrossTabulate[
      Flatten[Table[{"team:" <> ToString[ti], 
          "course:" <> ToString[ci], ctg[ci, ti, gi]}, {ti, nt}, {ci, 
          nc}] /. sol, 1]]];
   Do[If[(ch[ci, ti, gi] /. sol) == 1, 
     mf[[1, ti, ci]] = Style[mf[[1, ti, ci]], Red]], {ti, nt}, {ci, nc}];
   mf
   }],
 {gi, gnzInds}]

enter image description here

Visualize the solution

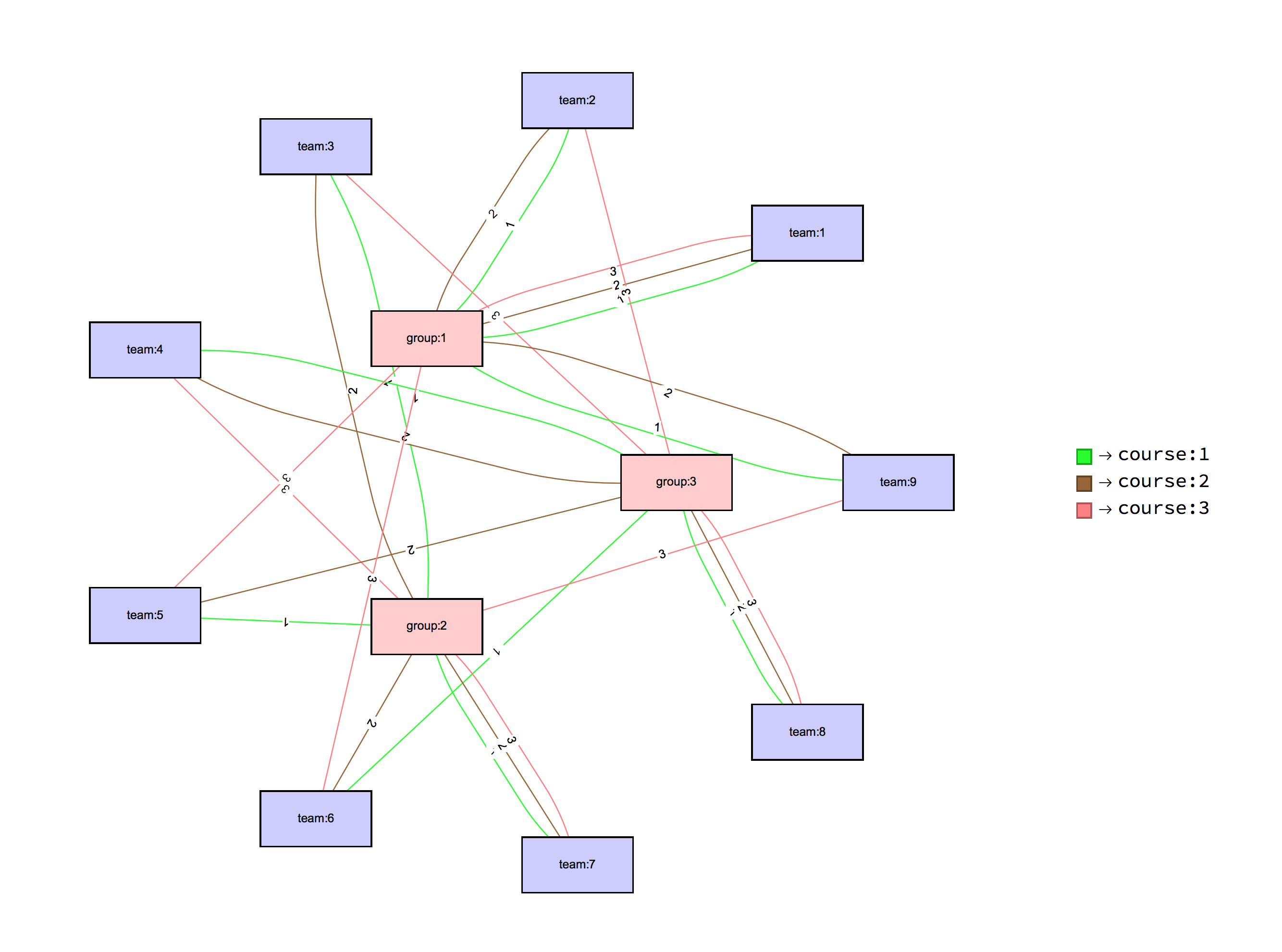
Here is a solution visualization with a graph plot:

graphEdges = 
  Map[Labeled[("team:" <> ToString[#[[2]]]) -> ("group:" <> 
        ToString[#[[3]]]), "course:" <> ToString[#[[1]]]] &, 
   Cases[sol, HoldPattern[ctg[___] -> 1], \[Infinity]][[All, 1]]];

vertices = Union[Flatten[List @@@ graphEdges[[All, 1]]]];

vcoords =
  Join[
   Block[{t = Flatten@StringCases[vertices, "group:" ~~ ___]}, 
    MapIndexed[# -> 0.3 {Cos[#2[[1]] 2 \[Pi]/Length[t]], Sin[#2[[1]] 2 \[Pi]/Length[t]]} &, t]], 
   Block[{t = Flatten@StringCases[vertices, "team:" ~~ ___]}, 
    MapIndexed[# -> 0.7 {Cos[#2[[1]] 2 \[Pi]/Length[t]], Sin[#2[[1]] 2 \[Pi]/Length[t]]} &, t]]
   ];

Legended[
 GraphPlot[List @@@ graphEdges,
  MultiedgeStyle -> All,
  VertexRenderingFunction -> ({If[StringMatchQ[#2, "team:" ~~ __], 
       RGBColor[0.8, 0.8, 1], RGBColor[1, 0.8, 0.8]], EdgeForm[Black],
       Rectangle[# - {0.1, 0.05}, # + {0.1, 0.05}], Black, 
      Text[#2, #1]} &),
  VertexCoordinateRules -> vcoords,
  EdgeRenderingFunction -> (With[{cind = 
        ToExpression[
         StringCases[#3, "course:" ~~ x__ :> x][[1]]]}, {{Green, 
         Brown, Pink}[[cind]], Line[#], Black, 
       Inset[cind, Mean[#], Automatic, Automatic, #[[1]] - #[[2]], 
        Background -> White]}] &),
  ImageSize -> 900],
 Thread[{Green, Brown, Pink} -> 
   Map["course:" <> ToString[#] &, Range[nc]]]]

enter image description here
POSTED BY: Anton Antonov
12 Replies
Sort By:

Hello Maxime,

thank you very much for your answer. Seems I was not completely wrong. Good to know ;-). Looks like Anton is very busy at the moment. Hope he has some time in the future to help me for the last questions. That would be great. Or maybe there is someone else in this forum who knows the answers my questions above :-)

Regards,

Peter
POSTED BY: Peter Parker

Hi

Thank you very much for your reply!

If I rerun the code with the new package (or use the definition from your last post) I finally get a table: enter image description here However, as you can see, the table is not identical to the one you have and I still get some error messages.

Best regards,

Peter
POSTED BY: Peter Parker
Updating Name
Updating Name
Posted 8 years ago

Hello,

meanwhile I came to the conclusion (after checking several steps in this and similar Mathematica-codes), that loading the Mathematica file is not the reason for my error message. I now start to doubt if the very last section in the code above, the part where you plot the Matrix, is correct. It always tells me that one part of the matrix does not exist. And I don't understand why. Is there some other way to plot the data? I was thinking to export the result in an Excel file. The advantage is, that I can use the excle file for some other calculations.

I would really appreciate any help on this problem!

Thank you very much in advance!

Peter
POSTED BY: Updating Name

I can investigate this in more detail in the coming weekend.
POSTED BY: Anton Antonov

Hello Anton,

I would appreciate your help very much!!!

Thank you very much in advance!

Peter

POSTED BY: Peter Parker

Hey Anton,

looks like you are the only person who can help me with this problem....

Since the problem seems to work in your case, I hope we are close to a final solution for this.

I may have some further questions, but I want to ask them step by step. Highest priority has to plot the table. Either in Mathematica or in Excel. Both is fine for me. Excel maybe even more useful for post processing.

The code you have written is quite powerful and I already have an idea to improve it even more. But this would be the next step.

Cheers,

Peter
POSTED BY: Peter Parker

I did not include in my GitHub package MathematicaForPredictionUtilities.m the up-value definition of MatrixForm for Association objects that have keys "XTABMatrix" or "XTABTensor". I did that today. (Although I am not sure it is a good idea.) Please rerun your code with the new package definition or use the definition:

Unprotect[Association];
MatrixForm[x_Association /; (KeyExistsQ[x, "XTABMatrix"] || KeyExistsQ[x, "XTABTensor"])] ^:= (MatrixForm[#1, TableHeadings -> Rest[{##}]] & @@ x);
Protect[Association];
POSTED BY: Anton Antonov

Sorry, its me again :-)

I am confused. It is nice to see, that I am now able to get a table by running your code. This is great and I am thankful for all your help!!! But there are still some thinks that make me confuse:

1) Why do you get a different table? Maybe there are multiple solutions?

2) As you can see in my table (see screenshot), I do not have a chef team assignment for every course (red number missing). Therefore sth. must be wrong.

3) As you can see in the screenshot, I still get error messages.

4) Why does it obviously work in your case but not in my case? Am I doing sth. wrong or is it the code?

The algorithm is quite complex. I get most of it. I can follow the main steps, but I don't understand all the details (yet). Therefore I can not judge if I do sth. wrong or just the code. But how can I do sth. wrong when all I have to do is to run your code? This should not be so difficult.

Best regards,

Peter
POSTED BY: Peter Parker
Maxime Denker
Maxime Denker
Posted 8 years ago

Hi Peter

1) Yes looks like there are multiple solutions. At least both yours and Antons solution look right to me. When I run the code I get an other table as well.

2,3) The error messages are related to your problem. I get the same when I run the code. Don't really see what is the reason for this.

4) I don't know

Hope I could help you.

POSTED BY: Maxime Denker

Hi everyone,

I am still in the process of understanding the code step by step. So far I doing well but I have a problem after plotting the matrix (which, by the way, looks exactly like in the example). The problem appears with importing the Mathematica file. Please have a look at the screenshot.

![enter image description here][1]

Hope you can help me. As I sad, my Matrix plot looks like the one from the example, therefore I think this is not the problem.

Best regards,

Peter
POSTED BY: Peter Parker

For the Sudoku problem, I used FindMinimum to do the linear programming. I believe it selects that method automatically when the problem is linear.
POSTED BY: Frank Kampas

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations! We are happy to see you at the top of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract