I was thinking on Langton's Ant -- what if we used different angles instead of the square, triangular, or hexagonal grids? The concept of drop/take flags would need to change, and that can be done with a distance parameter.
loc = {0, 0};
pts = {};
drops = {};
currentangle = 0;
Monitor[Do[
If[Length[pts] > 0 ,
near = Nearest[pts, loc][[1]];
place = Flatten[Position[pts, near]][[1]];
dist = N[EuclideanDistance[near, loc]],
dist = 20];
If[dist < .15,
drops = Append[drops, pts[[place]]];
pts = Drop[pts, {place}];
currentangle = currentangle - 2 Pi/5;
loc = Chop[loc + N[{Sin[currentangle], Cos[currentangle]}]],
pts = Append[pts, loc];
currentangle = currentangle + 2 Pi/5;
loc = loc + N[{Sin[currentangle], Cos[currentangle]}]],
{g, 1, 3000}], g]
It happens to make a highway.
Graphics[{Line[pts], Point /@ drops}]
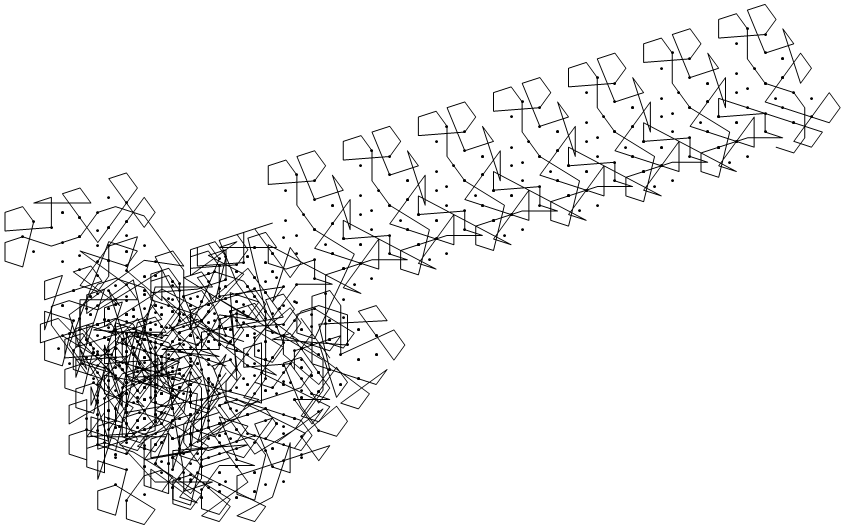
With angle set {-2 Pi/5, 2 Pi/5) and distance .15, the ant eventually makes a highway.
What other angle sets and distance parameters make highways?
For the adventuresome, use flags of different colors, and go into full turmite explorations.