I was thinking on Langton's Ant -- what if we used different angles instead of the square, triangular, or hexagonal grids? The concept of drop/take flags would need to change, and that can be done with a distance parameter.

loc = {0, 0};   
pts = {};  
drops = {};  
currentangle = 0;  
Monitor[Do[  
If[Length[pts] > 0 ,  
near = Nearest[pts, loc][[1]];  
place = Flatten[Position[pts, near]][[1]];  
dist = N[EuclideanDistance[near, loc]],  
dist = 20];  
If[dist < .15,  
drops = Append[drops, pts[[place]]];  
pts = Drop[pts, {place}];  
currentangle = currentangle - 2 Pi/5;  
loc = Chop[loc + N[{Sin[currentangle], Cos[currentangle]}]],  
pts = Append[pts, loc];  
currentangle = currentangle + 2 Pi/5;  
loc = loc + N[{Sin[currentangle], Cos[currentangle]}]],  
{g, 1, 3000}], g]  

It happens to make a highway.

Graphics[{Line[pts], Point /@ drops}]  

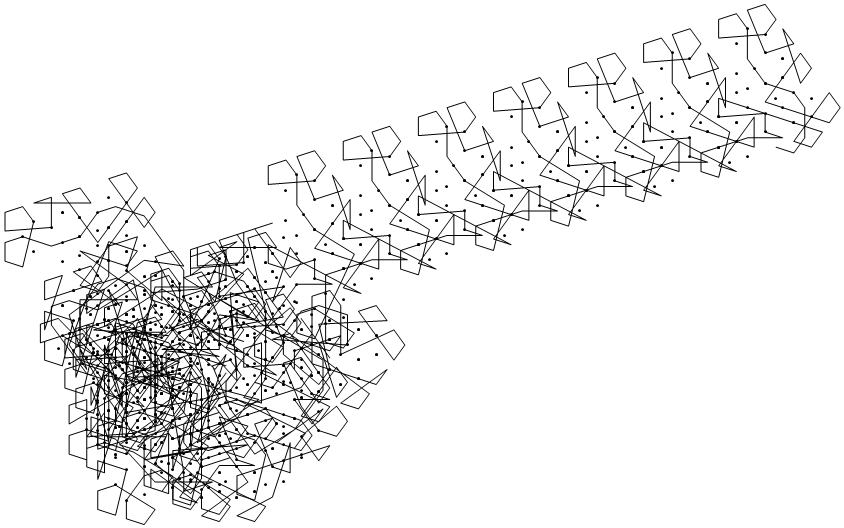
With angle set {-2 Pi/5, 2 Pi/5) and distance .15, the ant eventually makes a highway.

What other angle sets and distance parameters make highways?

For the adventuresome, use flags of different colors, and go into full turmite explorations.