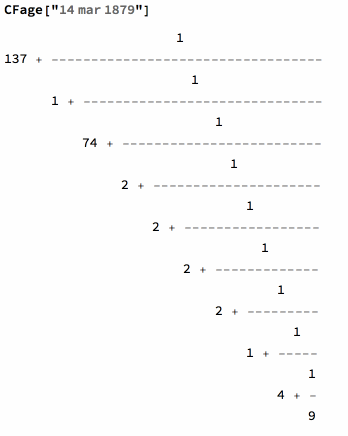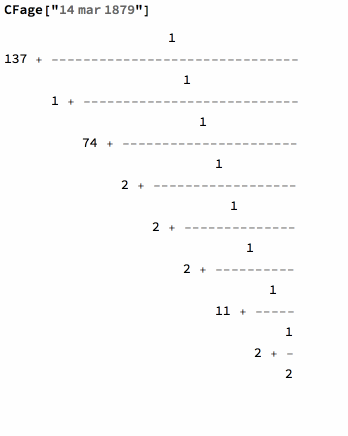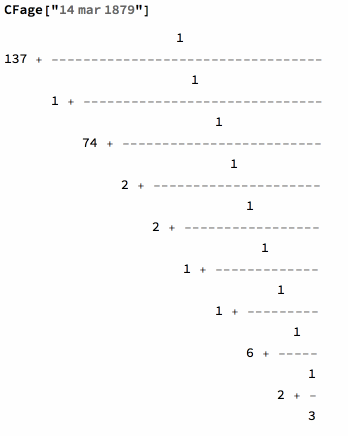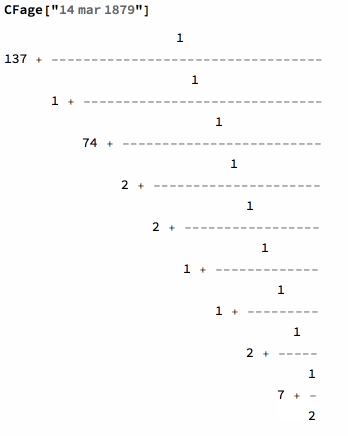
Your age as a continued fraction is given by the function CFage. It computes the difference between a birth date and the current time. Then this period is measured in years and transformed into a continued fraction. One can also give dates as integer lists right down to minutes and seconds. The number of terms is optional.
CFage[birthdate:(_String|_DateObject|{_Integer,___}),terms_:11]:=
Dynamic[
Fold[#2+1/#1&,
MapAt[
ToString,
Take[
ContinuedFraction[
DateDifference[birthdate,Now]/Quantity@"yr"],
UpTo[terms]]/.{a__,b_,1}:>{a,b+1}//Reverse,1]]//OutputForm,
UpdateInterval->.5]
Let's take Einstein birthday as an example:
The function CFage will work with such DateObject or it's String analog: