Hi Tim,
For physical modeling, have you ever considered using Wolfram SystemModeler? The system you describe can be modeled using drag-and-drop with prebuilt components:
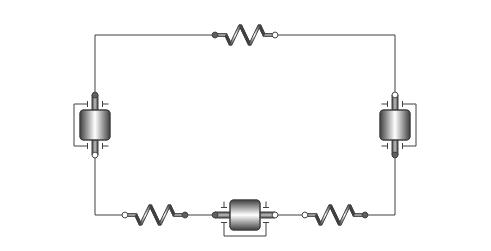
Then you can quite easily change parameters such as the spring constants, the masses or the number of masses. It can still be analyzed in Mathematica. Simulating the above model from Mathematica allows you to use the result right away.
sim = WSMSimulate["RotationalSprings"]
\[Theta]1[t_] := sim["I1.phi", t];
\[Theta]2[t_] := sim["I2.phi", t];
\[Theta]3[t_] := sim["I3.phi", t];
This can now work with the excellent code from Henrik above.
sim = WSMSimulate["RotationalSprings"]
\[Theta]1[t_] := sim["I1.phi", t];
\[Theta]2[t_] := sim["I2.phi", t];
\[Theta]3[t_] := sim["I3.phi", t];
angleSpring[\[Phi]1_, \[Phi]2_, n_Integer] := Module[{absDiff},
absDiff = Abs[\[Phi]2 - \[Phi]1];
If[absDiff < Pi,
ParametricPlot[(1 + .2 TriangleWave[n (\[Gamma] - \[Phi]1)/absDiff]) {Cos[\[Gamma]], Sin[\[Gamma]]}, {\[Gamma], \[Phi]1, \[Phi]2}, PlotRange -> {-1.3, 1.3}, PerformanceGoal -> "Quality"],
ParametricPlot[(1 + .2 TriangleWave[n (\[Gamma] - \[Phi]1)/(2 Pi + \[Phi]1 - \[Phi]2)]) {Cos[\[Gamma]], Sin[\[Gamma]]}, {\[Gamma], \[Phi]2 - 2 Pi, \[Phi]1},
PlotRange -> {-1.3, 1.3}, PerformanceGoal -> "Quality"]]
]
Animate[Show[angleSpring[\[Theta]1[time], \[Theta]2[time], 20],
angleSpring[\[Theta]2[time], \[Theta]3[time], 20],
angleSpring[\[Theta]1[time], \[Theta]3[time], 20],
Graphics[{Blue, Opacity[.85],
Disk[{Cos[\[Theta]1[time]], Sin[\[Theta]1[time]]}, 1/15],
Disk[{Cos[\[Theta]2[time]], Sin[\[Theta]2[time]]}, 1/15],
Disk[{Cos[\[Theta]3[time]], Sin[\[Theta]3[time]]},
1/15]}]], {time, 0, 120}, DisplayAllSteps -> True,
AnimationRate -> 3]
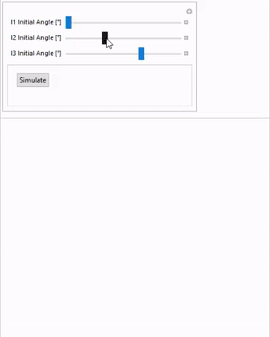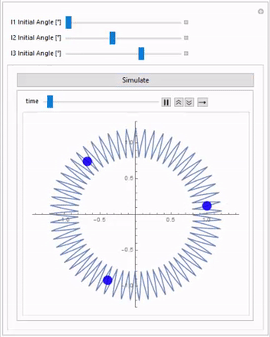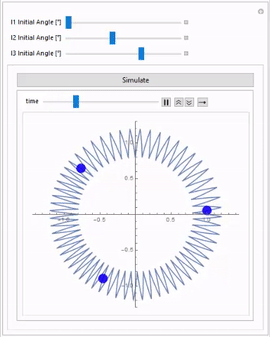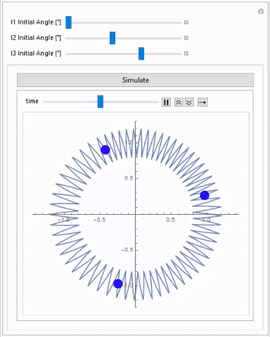
Using that, you could for example have a manipulate that gives you sliders to change different parts of the model. For example, here the initial angles of the masses are changed:
Manipulate[
Column[{
Button["Simulate", sim = WSMSimulate["RotationalSprings",
WSMInitialValues -> {"I1.phi" -> \[Phi]1, "I2.phi" -> \[Phi]2,
"I3.phi" -> \[Phi]3}]],
Animate[
Show[angleSpring[\[Theta]1[time], \[Theta]2[time], 20],
angleSpring[\[Theta]2[time], \[Theta]3[time], 20],
angleSpring[\[Theta]1[time], \[Theta]3[time], 20],
Graphics[{Blue, Opacity[.85],
Disk[{Cos[\[Theta]1[time]], Sin[\[Theta]1[time]]}, 1/15],
Disk[{Cos[\[Theta]2[time]], Sin[\[Theta]2[time]]}, 1/15],
Disk[{Cos[\[Theta]3[time]], Sin[\[Theta]3[time]]},
1/15]}]], {time, 0, 120}, DisplayAllSteps -> True,
AnimationRate -> 3]}], {{\[Phi]1, 0,
"I1 Initial Angle [\[Degree]]"}, 0, 360 Degree},
{{\[Phi]2, 120 Degree, "I2 Initial Angle [\[Degree]]"}, 0,
360 Degree},
{{\[Phi]3, 240 Degree, "I3 Initial Angle [\[Degree]]"}, 0, 360 Degree}
]
 Attachments:
Attachments: