Wolfram Alpha finds the same solutions:
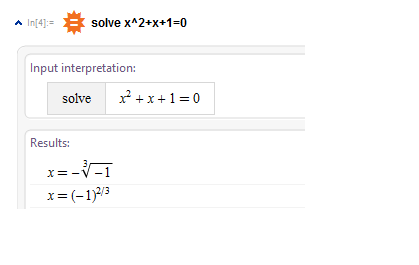
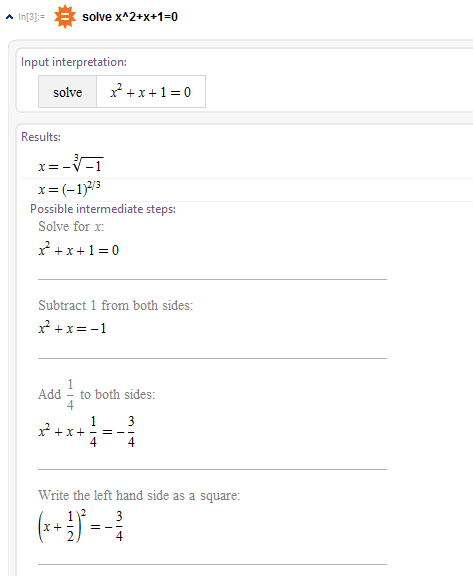
But, I used Step-by-step solution and found solution with the well known formula in the traditional form:
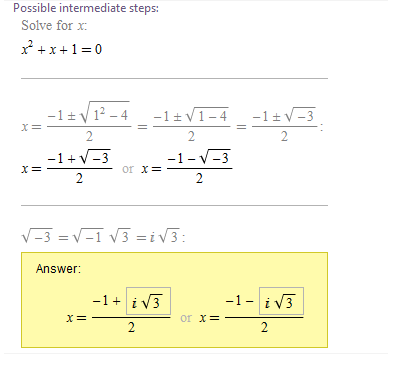
After that I used other variant of Step-by-step solution procedure and found the solution in the traditional form, too:

So, it's not clear why the result is presented in "non-traditional" form?
In[2]:= {{x -> -(-1)^(1/3)}, {x -> (-1)^(2/3)}} // FullForm
Out[2]//FullForm= \!\(TagBox[StyleBox[RowBox[{"List", "[", RowBox[{RowBox[{"List", "[", RowBox[{"Rule", "[", RowBox[{"x", ",",
RowBox[{"Times", "[", RowBox[{RowBox[{"-", "1"}], ",", RowBox[{"Power", "[", RowBox[{RowBox[{"-", "1"}], ",",
RowBox[{"Rational", "[", RowBox[{"1", ",", "3"}], "]"}]}], "]"}]}], "]"}]}], "]"}], "]"}], ",", RowBox[{"List", "[", RowBox[{"Rule", "[",
RowBox[{"x", ",", RowBox[{"Power", "[", RowBox[{RowBox[{"-", "1"}], ",", RowBox[{"Rational", "[", RowBox[{"2", ",", "3"}], "]"}]}], "]"}]}], "]"}], "]"}]}], "]"}],ShowSpecialCharacters->False,ShowStringCharacters->True,\NumberMarks->True], FullForm]\)
What is the reason to present solutions in an unusual "rational" form?