EDIT: See also the follow up posts here. and here.

Roughly 8-9 years ago a friend of mine told me I could make the Sierpinski triangle by starting at one of the vertices of an equilateral triangle, and then repeatedly jump half-way to one of the (randomly chosen) vertices.

0 memory

The following code will accomplish that:

ClearAll[sequence]
sequence[n_,m_]:=RandomChoice[Range[n],m]
pts=N@CirclePoints[3];
pts=FoldList[(#1+pts[[#2]])/2&,RandomChoice[pts],sequence[3,10]]
Graphics[{{FaceForm[],EdgeForm[Black],RegularPolygon[3]},Red,Arrow[Partition[pts,2,1]]}]

giving:

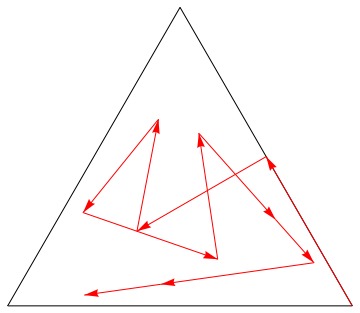
If one does this 1000s of time, and only mark the viewed points, one will get:

ClearAll[sequence]
sequence[n_,m_]:=RandomChoice[Range[n],m]
pts=N@CirclePoints[3];
pts=FoldList[(#1+pts[[#2]])/2&,RandomChoice[pts],sequence[3,25000]];
Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[3],PointSize[0.001],Point[pts]}]

giving:

Which will indeed show that by randomly choosing a vertex we can still get structure! Quite a surprise! Of course we can do this with squares, pentagons, hexagons et cetera:

ClearAll[sequence]
sequence[n_,m_]:=RandomChoice[Range[n],m]
Table[
    circlepoints=N@CirclePoints[n];
    pts=FoldList[(#1+circlepoints[[#2]])/2&,RandomChoice[circlepoints],sequence[n,50000]];
    Rasterize[Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[n],PointSize[0.001],Point[pts]},ImageSize->500,PlotRange->1.1],"Image"]
,
    {n,3,8}
] // Partition[#, 3] & // ImageAssemble

giving:

Very neat! (apart from 4, which just gives a homogeneous distribution of points). Here I run the pentagon many many points and high resolution to get:

Where now the gray-color represents the density of points.

0 memory - restricted

Now we can make the dynamics a bit more interesting by not moving to any other vertex but to only specific vertices. Imagine that we are at some position p, then we always have n choices (n being the number of sides): we can jump to the vertex 1 ahead, 2 ahead, .... n ahead (same as last time).

ClearAll[CreateSequence,CreateSequenceImage]
CreateSequence[n_,steps_,choices_]:=Mod[Accumulate[RandomChoice[choices,steps-1]~Prepend~1],n,1]
CreateSequenceImage[n_,m_,choices_]:=Module[{seq,pts},
    seq=CreateSequence[n,m,choices];
    pts=N@CirclePoints[n];
    seq=FoldList[(#1+pts[[#2]])/2&,First[pts],seq];
    Rasterize[Graphics[{PointSize[0.001],Point[seq]},ImageSize->500,PlotRange->1],"Image",RasterSize->{300,300}]
]

For a 3 sided polygon (i've been told these are called triangles) we can jump 1, 2, or 3 ahead or subsets of that:

Grid[Join@@@Partition[{#,CreateSequenceImage[3,10^5,#]}&/@Subsets[Range[3],{1,\[Infinity]}],UpTo[3]],Frame->All]

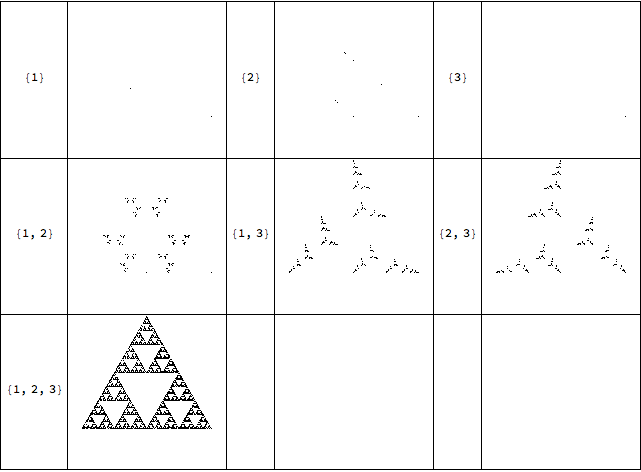
Some interesting structure can be seen for some of the subsets.

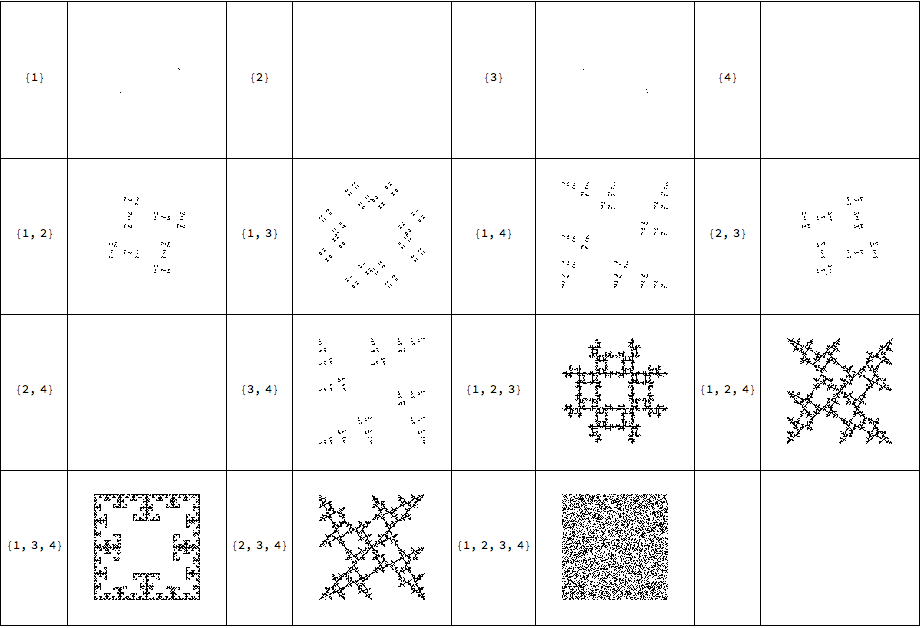
For squares:

Grid[Join@@@Partition[{#,CreateSequenceImage[4,10^5,#]}&/@Subsets[Range[4],{1,\[Infinity]}],UpTo[4]],Frame->All]

and for pentagons:

Grid[Join@@@Partition[{#,CreateSequenceImage[5,10^5,#]}&/@Subsets[Range[5],{1,\[Infinity]}],UpTo[4]],Frame->All]

the higher the number of sides, the more subsets we can choose. The number of subsets scales as 2^n -1 (minus one because the set can not be empty; we have to jump somewhere!).

Lastly, for hexagons:

Grid[Join@@@Partition[{#,CreateSequenceImage[5,10^5,#]}&/@Subsets[Range[5],{1,\[Infinity]}],UpTo[4]],Frame->All]

Ok, you can try polygons with large number of sides on your own, but note that the number of subsets doubles every time.

1 memory - restricted

We can even go beyond this, and consider the position of the penultimate vertex as well:

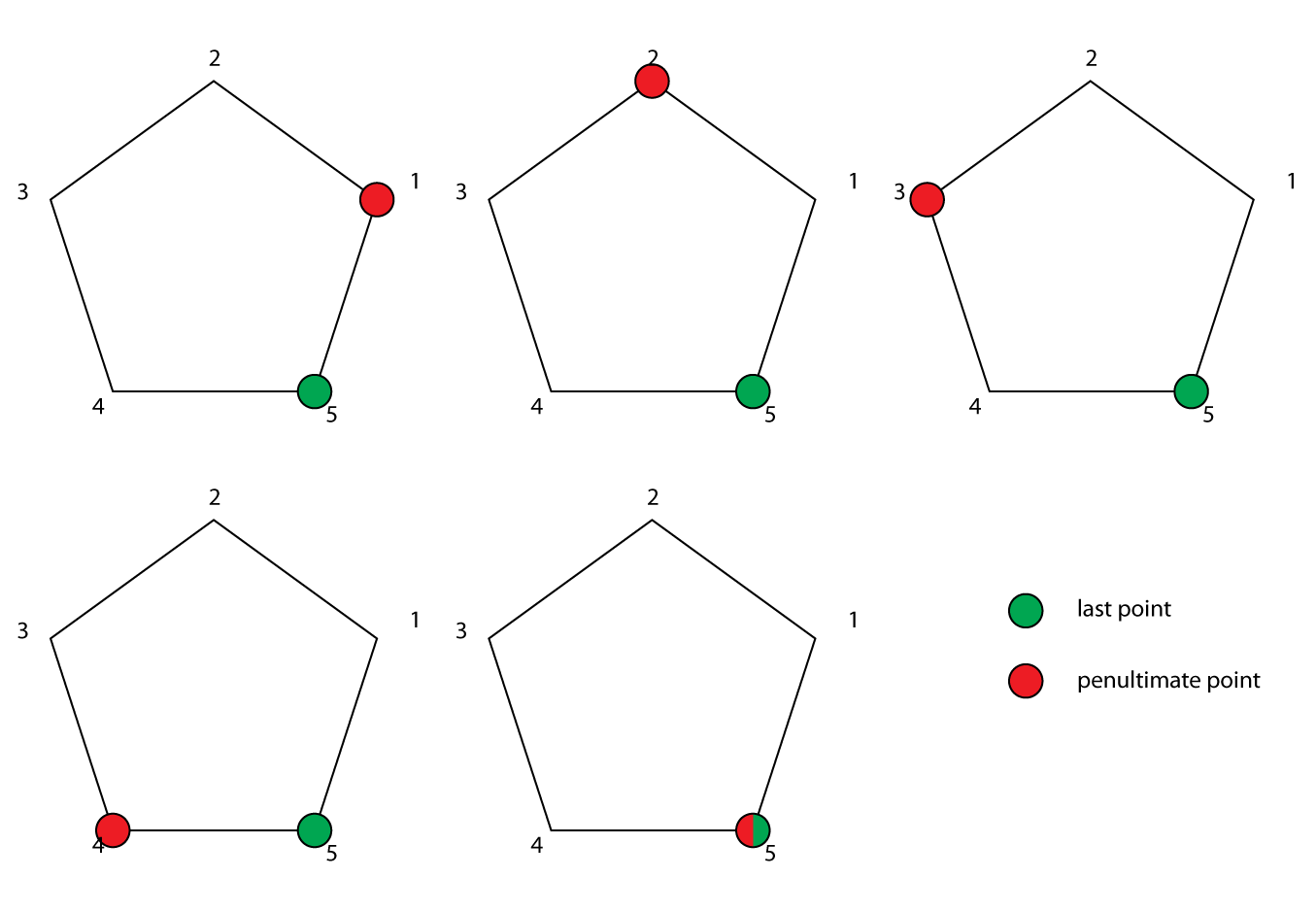
We can consider 5 cases for a pentagon (or, in general, n cases). We will consider the last point to be at position 0 (or n), now the penultimate vertex could be in 5 different positions. For each of these combinations we can choose a different subset of {1,2,3,4,5}. Just to get an idea how many possibilities we now have:

the number of subsets is 2^n - 1, and we have to choose n of these, so there will be (2^n-1)^n different systems to explore:

Table[{n, (2^n - 1)^n}, {n, 3, 8}] // Grid

as one can see, the combination grow very quickly.

ClearAll[Stamp,CreateSequence2,CreateSequenceImage2]
CreateSequence2[n_,m_,start:{start1_,start2_},choices_]:=Module[{out,last, penultimate,new,pos2},
    {penultimate,last}=out=start;
    out=Reap[Do[
        pos2=Mod[penultimate-last,n,1];
        new=Mod[last+RandomChoice[choices[[pos2]]],n,1];
        penultimate=last;
        last=new;
        Sow[new]
    ,
        {m-2}
    ]][[2,1]];
    Join[start,out]
]
Stamp[n_,choices_]:=Module[{},
    Image[Normal[SparseArray[Thread[Join@@MapThread[Thread[{#1,#2}]&,{Range[Length[choices]],choices}]->1],{n,n}]]]
]
CreateSequenceImage2[n_,m_,start:{start1_,start2_},choices_]:=Module[{seq,pts,ras,stamp},
    seq=CreateSequence2[n,m,start,choices];
    pts=N@CirclePoints[n];
    seq=FoldList[(#1+pts[[#2]])/2&,First[pts],seq];
    ras=Rasterize[Graphics[{PointSize[0.001],Point[seq]},ImageSize->500,PlotRange->1],"Image",RasterSize->{300,300}];
    stamp=ImagePad[Stamp[n,choices],1,Red];
    ImageCompose[ras,stamp,{Center,Bottom},{Center,Bottom}]
]

Before looking at the general case, we can look at a small subset, namely one can not jump i ahead from the last, and j ahead from the penultimate. Here the example for i=1, and j =3:

ClearAll[JumpPos2]
JumpPos2[n_,{d1_,d2_}]:=Module[{pos},
    pos=Range[n];
    pos=DeleteCases[pos,d1];
    DeleteCases[pos,Mod[d2+#,n,1]]&/@Range[n]
]
CreateSequenceImage2[4,10^4,{1,2},JumpPos2[4,{1,3}]]

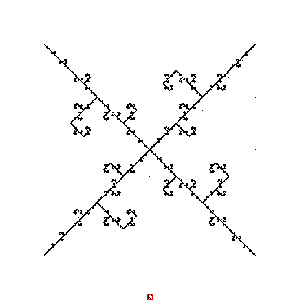
Very neat structure! Of course we can try all i and j from the set {1,2,3,4}:

delta=Tuples[Range[4],2];
deltas=JumpPos2[4,#]&/@delta;
Grid[Join@@@Table[{{i,j},CreateSequenceImage2[4,10^4,{1,2},JumpPos2[4,{i,j}]]},{i,4},{j,4}],Frame->All]

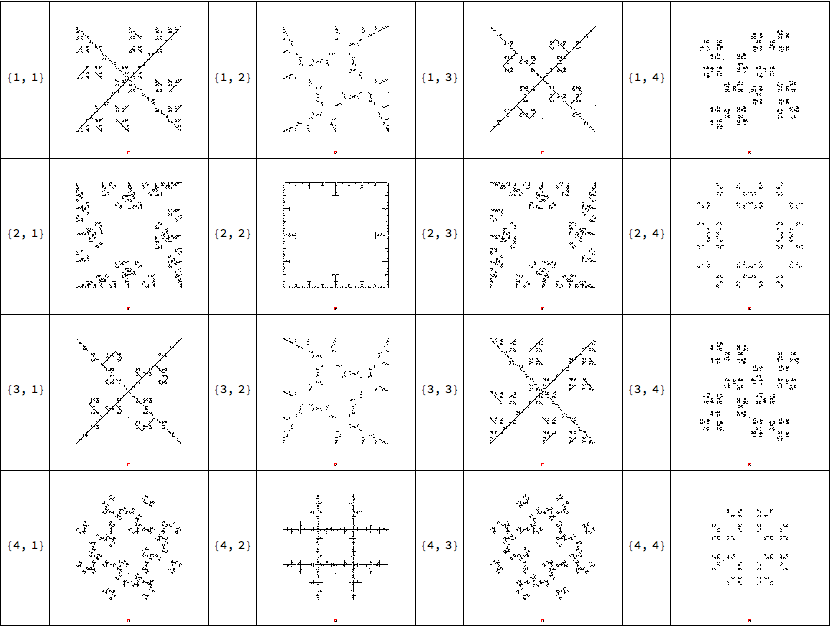
All very neat, but it is just a small subset of the 50625 possibilities. Here let's try 64 random ones:

sc=Reverse@Subsets[Range[4],{1,\[Infinity]}];
Table[
   CreateSequenceImage2[4,10^4,{1,2},RandomChoice[sc,4]]
,
    {64}
] // Partition[#,8]& // ImageAssemble

As you can see very nice and rich structure! Notice that I 'stamped' all of them with their 'input':

CreateSequenceImage2[4, 10^4, {1, 2}, {{1, 4}, {3}, {1, 3, 4}, {1, 2, 3}}]

And if one looks closely (save the image and zoom), one will see the 'stamp' (or the rule) at the bottom:

This can be read as follows:

• The first (top) line, the white pixels are in places 1 and 4, so if the penultimate vertex was '1', move 1 or 4 places from the last vertex
• The 2nd line, the white pixel is in place 3, jump the position 3 ahead compared to last vertex
• 3rd line, white pixel at 1,3, and 4.
• 4th line 1, 2, or 3.

Basically the nth line corresponds to the position of the penultimate vertex. and the white pixels corresponds to 'allowed' number of jumps.

I'll stop here for now. There are many more ideas to explore, I'll name a few:

• 3D positions, 3D images See below the post of Henrik!
• Anything other than regular polygons
• Have different probabilities for each of the vertices...
• Move in the perpendicular direction
• ...

See also the follow up posts here. and here and some additional visualizations below!