I have got a specific LP optimization problem as attached picture.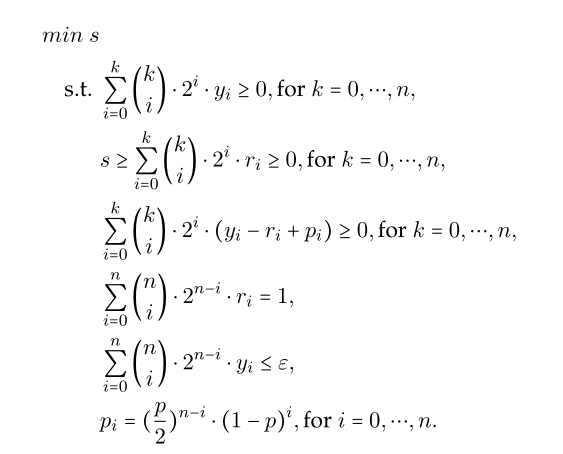
Given a integer n and $\varepsilon,\ p \in (0,1)$, this is a LP optimization over 2n+3 variables. I am trying to solve this with Mathematica LinearProgramming function. When n is less than 18, everything is fine and it gives an optimal solution. But when n is greater or equal than 19, it gives an warning that "no solution can be found that satisfies the constraint".

Apparently, there is feasible solution that $y_i = 0$ and $r_i = p_i$. I believe that Mathematica can handle hundreds of variables without doubt.
But why it does not give a solution when n is over 19 in this case? Btw, I have also posted this problem on Stackexchange Mathematica which can be found here (http://mathematica.stackexchange.com/questions/139976/linearprogramming-function-cannot-find-a-feasible-solution).
My code is as followed:
ClearAll["Global`*"];
n = 3; e = 0.01; p = 2/3;
u[k_,i_]:=If[k>=i,Binomial[k,i]*2^i,0];
c = Table[u[i,j],{i,0,n},{j,0,n}];
zblock = SparseArray[{},{n+1,n+1}];
zcolum = SparseArray[{},{n+1,1}];
ones = ConstantArray[1,{n+1,1}];
(*Constraints*)
c1 = Join[c,zblock,zcolum,2];
c2 = Join[zblock,c,zcolum,2];
c3 = Join[zblock,-c,ones,2];
c4 = {Flatten[Join[SparseArray[{},{1,n+1}],Reverse[c[[n+1]]],{0}]]};
c5 = {Flatten[Join[Reverse[c[[n+1]]],SparseArray[{},{1,n+1}],{0}]]};
c6 = Join[c,-c,zcolum,2];
M = Join[c1,c2,c3,c4,c5,c6];
(*Objective*)
ob = Flatten[Join[SparseArray[{},{1,2*(n+1)}],{{1}},2]];
(*Bounds*)
b1 = ConstantArray[{0,1},3*(n+1)];
b2 = {{1,0},{e,-1}};
(*b31 = {Table[-Sum[Binomial[k,i]*2^i*(p/2)^(n-i)*(1-p)^i,{i,0,k}],{k,0,n}]};*)
(*b31 = {Table[-(p/2)^(n-k)*(2-3*p/2)^k,{k,0,n}]};*)
b31 = {Table[-(1/3)^(n-k),{k,0,n}]};
b3 = Join[Transpose[b31],ones,2];
bounds = Join[b1,b2,b3];
bounds[[All,1]] = Total[M[[All,1;;2*n+2]],{2}]+bounds[[All,1]];
ob = SparseArray[ob];
L = LinearProgramming[ob,M,bounds];
ob.L
Note: this problem has been solved by replacing e = 0.01 to e = 1/100 as suggested by Mr. Lichtblau.