The general formula created for symbolic x seems to contain an error unfortunately:
sol = Integrate[Abs[x - y]*(1 - Abs[y]), {y, -1, 1}]
num = Table[{x, NIntegrate[Abs[x - y]*(1 - Abs[y]), {y, -1, 1}]}, {x, -2, 2, 0.1}]
Show[{Plot[sol, {x, -2, 2}], ListPlot[num]}]
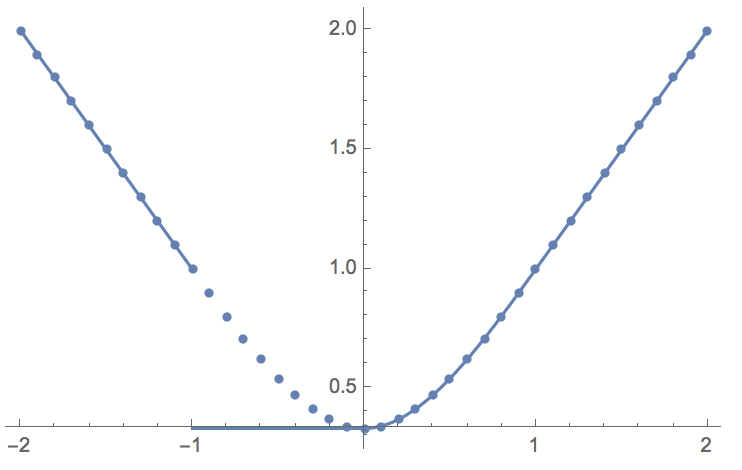
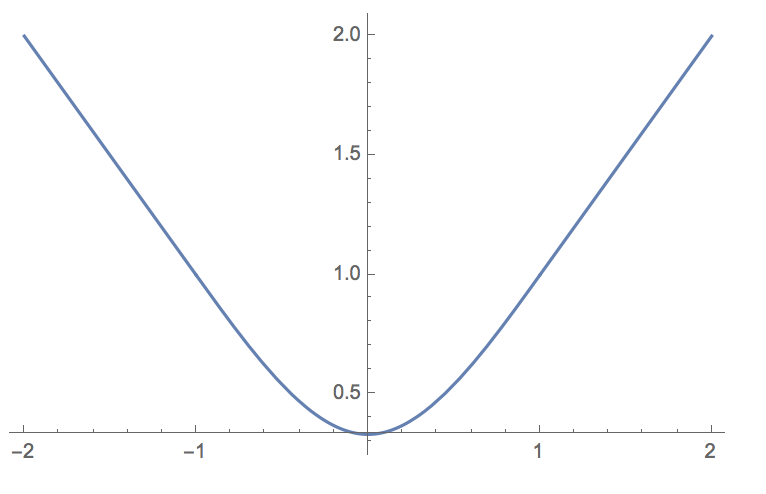
If you explicitly specify x to be a real number the answer is correct:
Integrate[Abs[x - y]*(1 - Abs[y]), {y, -1, 1}, Assumptions -> x \[Element] Reals]
Plot[%, {x, -2, 2}]
Submitted as product feedback (CASE:3868504) with the following minimal working example:
f=-Abs[y-x] Abs[y] (* without the minus in front it is ok actually !! *)
sol=Integrate[f,{y,-1,1}];
numsol=Table[{x,NIntegrate[f,{y,-1,1}]},{x,-2,2,0.1}];
Show[{ListPlot[numsol],Plot[sol,{x,-2,2}]}]
(* with the assumption that x is a real number it is ok *)
f=-Abs[y-x] Abs[y]
sol=Integrate[f,{y,-1,1},Assumptions->x\[Element]Reals];
numsol=Table[{x,NIntegrate[f,{y,-1,1}]},{x,-2,2,0.1}];
Show[{ListPlot[numsol],Plot[sol,{x,-2,2}]}]