The other day I was watching a video on the wonderful Numberphile channel about the illumation problem. Check it out here.

It's about light bouncing inside a closed room where all the walls are covered by mirrors. Roger Penrose came up with a room which can not be completely lit by a single light source. I was very curious what the paths would look like so here it is.

Let's first create the shape:

gr=Graphics[{Circle[{0,3},{10.,6.},{0,Pi}],Line[{{10,3},{10,0.5},{8,0.5},{8,3}}],Line[{{-10,3},{-10,0.5},{-8,0.5},{-8,3}}],Circle[{0,-3},{10.,6.},{Pi,2*Pi}],Line[{{10,-3},{10,-0.5},{8,-0.5},{8,-3}}],Line[{{-10,-3},{-10,-0.5},{-8,-0.5},{-8,-3}}],Circle[{8,0},{1.8,3.},{Pi/2,(3*Pi)/2}],Circle[{-8,0},{1.8,3.},{(3*Pi)/2,(5*Pi)/2}]},Frame->True];
gr=gr/.((c:Circle[__]):>MeshPrimitives[DiscretizeRegion[c,MaxCellMeasure->0.0003],1]);
gr=gr/.Line[x_?(Length[#]>2&)]:>(Line/@Partition[x,2,1]);
lines=Cases[gr,Line[x_]:>x,\[Infinity]];
lines//Length
Graphics[Line[lines]]

Note that I discretize the ellipses with a small measure, such that we have a very good approximation. What I'm left with is only small line pieces.

Here is some code that calculates the paths (not optimized, I'll leave that to someone else; I'm sure some operations can be vectorized):

ClearAll[LineLineIntersect, JumpAroundCreateGraphics]
LineLineIntersect[X1_, X2_, X3_, X4_] := 
 Module[{a, denom, \[CapitalDelta]x, x2, x4, \[CapitalDelta]y, y2, y4},
  {\[CapitalDelta]x, \[CapitalDelta]y} = X1 - X3;
  {x2, y2} = X2;
  {x4, y4} = X4 - X3;
  denom = x4 y2 - x2 y4;
  If[denom == 0, Return[False],
   a = (y4 \[CapitalDelta]x - x4 \[CapitalDelta]y)/denom;
   If[a > 10^-10 \[And] 
     0 <= (y2 \[CapitalDelta]x - x2 \[CapitalDelta]y)/denom <= 1, 
    Return[a], Return[False]]
   ]
  ]
JumpAroundCreateGraphics[lines_, n_, dirs_List, start_] := 
 Module[{points, k, cp, cv, dat, fdat, tmp, index, np, mirror},
  k = 0;
  PrintTemporary[ProgressIndicator[Dynamic[k/(Length[dirs] n)]]];
  points = Table[
    cp = start;
    cv = \[Theta];
    Reap[
      Sow[cp];
      Do[
       k++;
       dat = LineLineIntersect[cp, cv, #1, #2] & @@@ lines;
       fdat = Min @@ DeleteCases[dat, False];
       tmp = Flatten[Position[dat, fdat]];
       If[Length[tmp] > 0,
        index = First[tmp];
        np = cp + dat[[index]] cv;
        mirror = (#[[2]] - #[[1]]) &[lines[[index]]];
        cv = -cv + 2 (cv.mirror/Norm[mirror]) (mirror/Norm[mirror]); 
        Sow[cp = np]
        ]
       ,
       {i, n}
       ]
      ][[2, 1]]
    ,
    {\[Theta], dirs}
    ];
  Graphics[{Line@lines, Line /@ points, Red, 
    Arrow /@ points[[All, ;; 2]], Blue, Disk[start, 0.25]}, 
   AspectRatio -> Automatic]
  ]

We can try it out by calling this new function:

JumpAroundCreateGraphics[lines, 15, {{1.2, -0.4}}, {0.5, 0.5}]

where lines is all the little line-pieces, 15 the number of bounces, followed by a list of directions, and lastly the starting position.

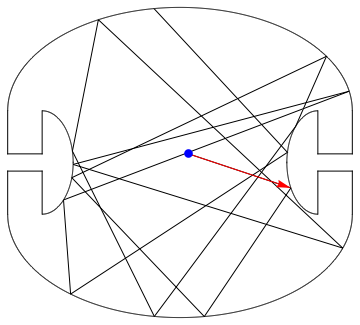
We can run it longer and indeed confirm that the four square corners will not be lit if we start somewhere in the middle:

JumpAroundCreateGraphics[lines, 150, {{1.2, -0.4}}, {0.5, 0.5}]

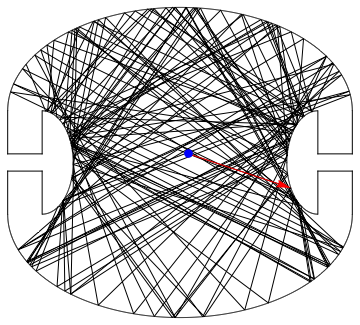
Indeed, the corners remain in the dark.

A more comprehensive search is by sending light out in more than one direction:

JumpAroundCreateGraphics[lines, 25, CirclePoints[12], {0.5, 0.5}]

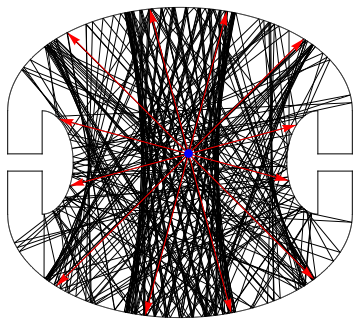
We can see again that the corners stay in the dark.

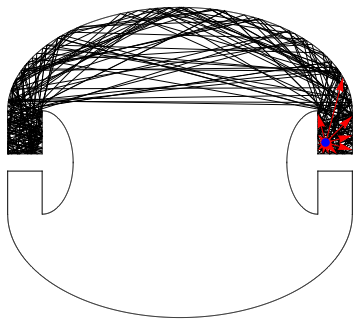
If we start in one of the corners only part of the box is illuminated:

JumpAroundCreateGraphics[lines, 25, CirclePoints[12], {8.45, 1.15}]

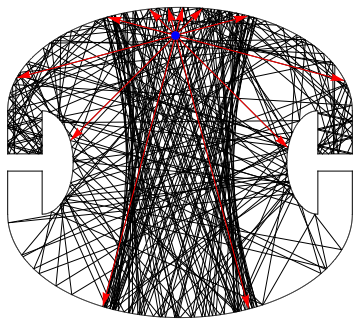
And lastly, if we start in the top half-ellipse, it will reach only the top 2 corners:

JumpAroundCreateGraphics[lines, 25, CirclePoints@12, {-0.2632, 7.377}]

Final note: note that I used a discretized version of the ellipses, after many many bounces the effect of this will show up and accumulate errors slowly. So if one calculates many many bounces it will end up everywhere...

Hope you enjoyed this little exploration.