A few weeks ago I was watching the excellent Numberphile video on the game of Frog Jumping:

Watch it here if you haven't already.

The video talks about the frog-jumping puzzle. Imagine a line of lily pads:

Lilypad[p:{x_,y_},s_]:=Scale[FilledCurve[BSplineCurve[(#+p)&/@{{0,0.25},{0,1},{1,1},{1,-0.75},{-1,-0.75},{-1,1},{0,1},{0,0.25}}]],s,p]
Graphics[{EdgeForm[{Thick, Black}], FaceForm[RGBColor[0, 0.5, 0]], Lilypad[{#, 0}, 0.3] & /@ Range[5]}]

the puzzle start with one frog on each lilypad, which I will denote with 1's above the lilypad:

Graphics[{EdgeForm[{Thick,Black}],FaceForm[RGBColor[0,0.5,0]],{Lilypad[{#,0},0.3],Text[Style[1,14],{#,1}]}&/@Range[5]}]

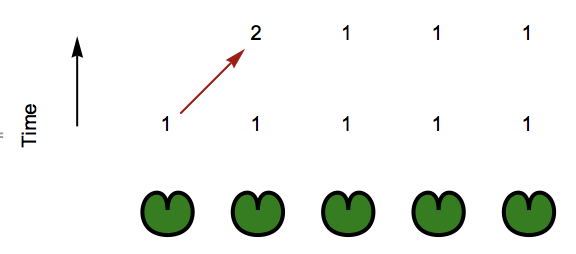
The goals of the puzzle is to land all the frogs on to the same lily pad. But there are rules: if there are n frogs on a certain lily pad these frogs can only jump n distance (either to the left or right). And all the frogs (from a certain lily pad) have to jump at once. And lastly, they can't jump onto an empty lily pad; once it is emptied, it can't be returned to.

I can now make one jump which will look like this:

VisualizeSequence[state_Association,height_]:=KeyValueMap[Text[#2,{#1,height}]&,state]
VisualizeSequences[states_List,enabled_]:=Module[{diff,startx,endx,y,arrows},
    diff=Partition[states,2,1];
    diff=Merge[#,Identity]&/@diff;
    startx=First[Keys[Select[#,Length[#]==1&]]]&/@diff;
    endx=First[Keys[Select[#,Length[#]==2\[And]Unequal@@#&]]]&/@diff;
    y=Range[Length[states]-1];
    arrows=MapThread[{{#1,#3},{#2,#3+1}}&,{startx,endx,y}];
    arrows={#1+0.2Normalize[#2-#1],#2-0.2Normalize[#2-#1]}&@@@arrows;
    Graphics[{
        {Darker@Red,Arrow/@arrows},
        MapIndexed[VisualizeSequence[#1,First[#2]]&,states],
        {EdgeForm[{Thick,Black}],FaceForm[RGBColor[0,0.5,0]],Lilypad[{#,0},0.3]&/@enabled},
        Arrow[{{Min[enabled]-1,1},{Min[enabled]-1,Length[states]}}],
        Text["Time",{Min[enabled]-1.5,(Min[enabled]-1+Length[states])/2},{0,0},{0,1}]
        },
        ImageSize->50(Max[enabled]-Min[enabled]+1.5)
    ]
]

states = {<|1 -> 1, 2 -> 1, 3 -> 1, 4 -> 1, 5 -> 1|>, <|2 -> 2, 3 -> 1, 4 -> 1, 5 -> 1|>};
VisualizeSequences[states, Range[5]]

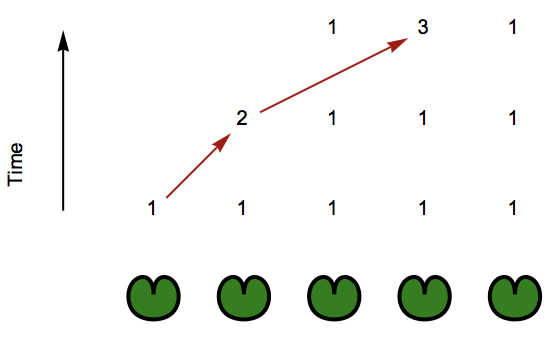
I can make another step now:

states={<|1->1,2->1,3->1,4->1,5->1|>,<|2->2,3->1,4->1,5->1|>,<|3->1,4->3,5->1|>};
VisualizeSequences[states,Range[5]]

And to finish it off:

states={<|1->1,2->1,3->1,4->1,5->1|>,<|2->2,3->1,4->1,5->1|>,<|3->1,4->3,5->1|>,<|4->4,5->1|>,<|4->5|>};
VisualizeSequences[states,Range[5]]

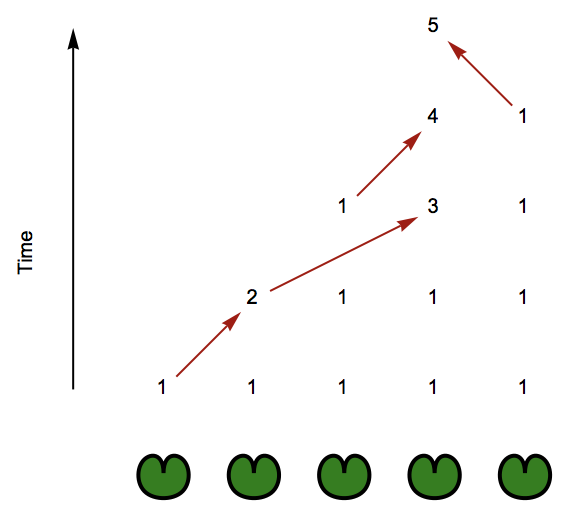
Solving the puzzle

The puzzle that was posed in the video is about the following arrangement:

Graphics[{EdgeForm[{Thick,Black}],FaceForm[RGBColor[0,0.5,0]],{Lilypad[{#,0},0.3],Text[Style[1,14],{#,1}]}&/@{1,3,4,5,7,8,9,11},Text[Style["\[Ellipsis]",14],{6,0}],Text[Style["\[Ellipsis]",14],{6,1}],Text[Style["n",14],{6,-1.5}],Arrowheads[{-0.05,0.05}],Arrow[{{1,-1},{11,-1}}]},PlotRangePadding->Scaled[.1],ImageSize->400]

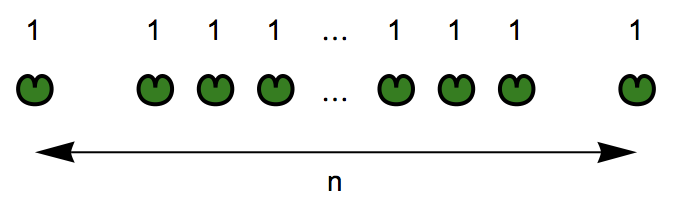
Where we have places 1 through n, where lily pad 2 and n-1 are gone; so we have n-2 active lily pads. Is this solveable for any n? We can write a simple solver now:

FrogSequences[state_] := Catch[PossibleFrogStates[state, {state}]]
PossibleFrogStates[state_, history_: {}] := Module[{futures},
  futures = Catenate[PossibleFrogStatesHelper[state, #] & /@ Keys[state]];
  Do[
   If[Length[f] == 1,
    Throw[Append[history, f]]
    ,
    PossibleFrogStates[f, Append[history, f]]
    ]
   ,
   {f, futures}
   ]
  ]
PossibleFrogStatesHelper[state_, key_] := Module[{val, newpos, tmp},
  val = state[key];
  newpos = {key - val, key + val};
  newpos = Intersection[newpos, Keys[state]];
  Table[
   tmp = state;
   KeyDropFrom[tmp, key];
   tmp[np] += val;
   tmp
   , {np, newpos}
   ]
  ]

Which we can try out by first trying to solve the above puzzle:

solution=FrogSequences[Association[#->1&/@Range[5]]]
VisualizeSequences[solution,Range[5]]

giving:

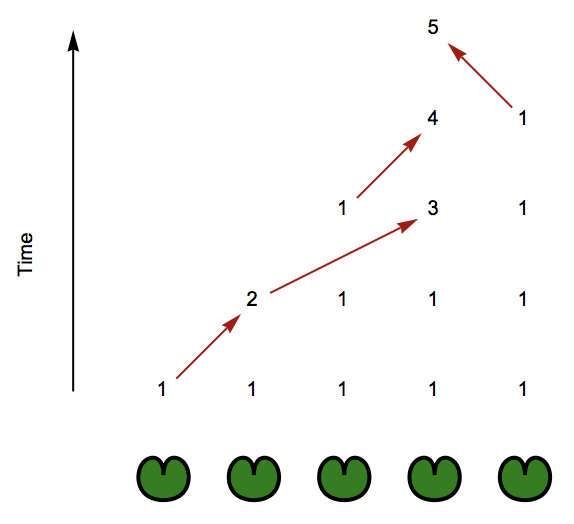
So now let's iterate over n (starting at 4) and stop until we find one that is solvable:

solution = Catch@Do[
    enabled = Delete[Range[n], {{2}, {-2}}];
    frogs = Association[# -> 1 & /@ enabled];
    sol = FrogSequences[frogs];
    If[sol =!= Null, Print[n, " = solvable!"]; Throw[sol]]
    ,
    {n, 4, 20}
    ];
VisualizeSequences[solution, enabled]

running the code finds that n = 12 is solvable:

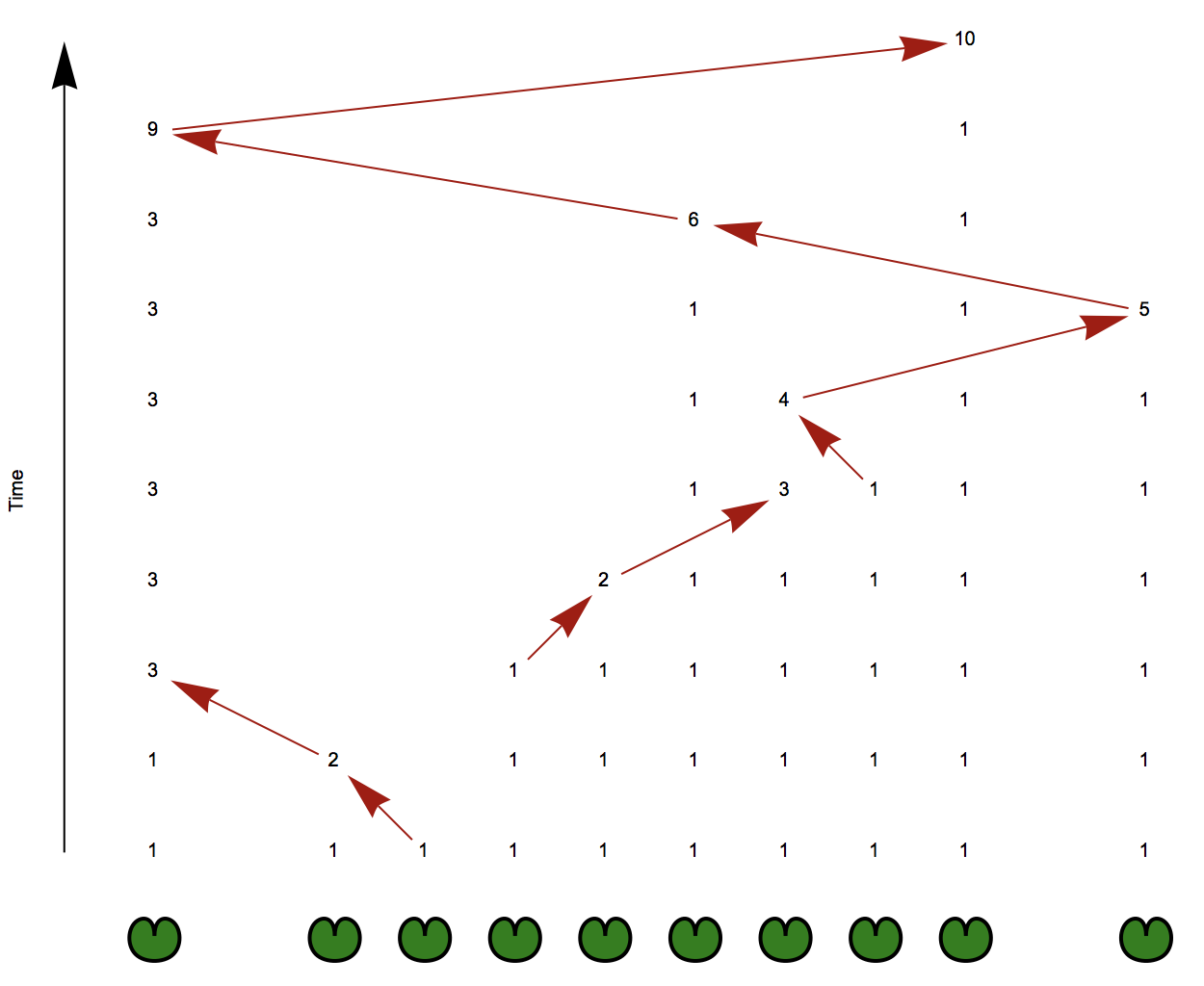
if you like this posts and you have another Numberphile video that needs the Wolfram Language treatment, let me know. Check also out the other Numberphile inspired post I did:

• [Numberphile] - The Illumination Problem
• [Numberpile] - Sandpiles - Done in the Wolfram Language