My first try would just be swapping pairs of connections until we have an optimum:
ClearAll[TrySwitch, TotalDistance, TrySwitch, FindPairs]
TotalDistance[pts_List, conns_List] := Total[Norm[N[pts[[#1]] - pts[[#2]]]] & @@@ conns]
TrySwitch[pts_List, conns_List, indices_List] := Module[{orig, newconns, subsets, ids},
orig = Sort[Sort /@ conns[[indices]]];
ids = Partition[#, 2] & /@ Permutations[Flatten[orig]];
ids = Union[Sort /@ Map[Sort, ids, {2}]];
ids = TakeSmallestBy[ids, TotalDistance[pts, #] &, 1][[1]];
newconns = Delete[conns, List /@ indices];
newconns~Join~ids
]
TrySwitchAll[pts_List, conns_List] := Module[{subsets, newerror, j = 0, olderror, newconns = conns},
subsets = Subsets[Range[Length[conns]], {2}];
newerror = 1;
olderror = -1;
While[olderror =!= newerror \[And] j < 1000 (* safeguard *),
j++;
Do[
newconns = TrySwitch[pts, newconns, s];
,
{s, subsets}
];
olderror = newerror;
newerror = TotalDistance[pts, newconns];
];
newconns
]
FindPairs[pts_List] := Module[{candidates, out, tmp, left},
If[EvenQ[Length[pts]] \[And] Length[pts] >= 2,
TrySwitchAll[pts, Partition[Range[Length[pts]], 2]]
,
Print["Even number of points >=2 needed!"]
]
]
Which works with your example:
pts = {{5, 0}, {7, 0}, {2, 3}, {0, 0}, {16, 14}, {3, 8}, {19, 5}, {18,
16}, {12, 0}, {19, 4}, {7, 3}, {0, 4}, {20, 3}, {5, 12}, {19,
8}, {11, 2}, {3, 10}, {4, 2}, {17, 11}, {15, 6}};
out = FindPairs[pts]
TotalDistance[pts, out]
Graphics[{Red, Point[pts], Black, Line[pts[[#]] & /@ out]}]
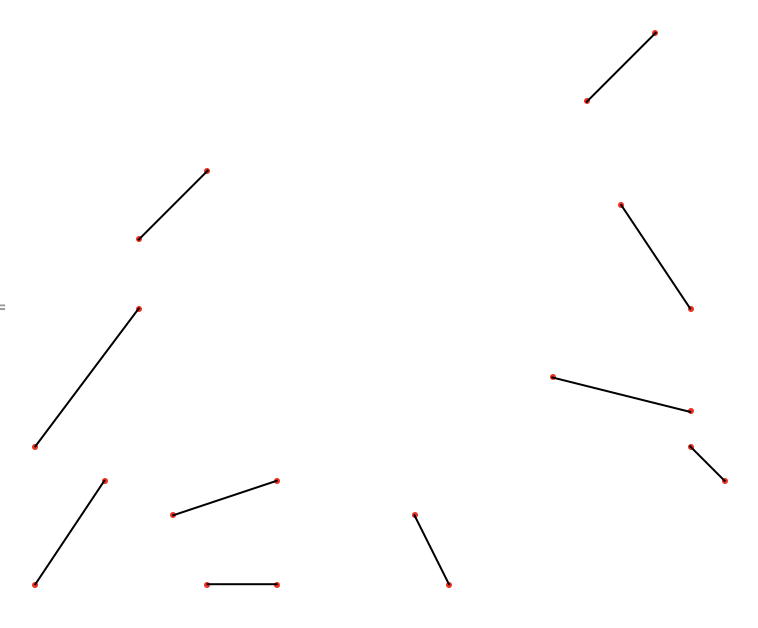
Total sum distance of distance: 30.8036
We can make it slightly smarter by starting with a more intelligent initial choice of pairs. Here I look for the nearest 7 neighbours of each point forming 7*n candidate pairs, we sort these candidates by distance, and then greedily pick them; shortest distance first. Only picking each point once...
ClearAll[FindPairs]
FindPairs[pts_List] := Module[{candidates, out, tmp, left},
If[EvenQ[Length[pts]] \[And] Length[pts] >= 2,
candidates = Transpose[{Range[Length[pts]], Nearest[pts -> "Index", pts, Min[Length[pts], 8]]}];
candidates = With[{x = #1, y = Rest[#2]}, {x, #} & /@ y] & @@@ candidates;
candidates = Join @@ candidates;
candidates = {#, TotalDistance[pts, #]} & /@ candidates;
candidates = SortBy[candidates, Last][[All, 1]];
out = Reap[While[Length[candidates] > 0,
tmp = candidates[[1]];
candidates = Rest[candidates];
candidates = DeleteCases[candidates, {___, tmp[[1]], ___} | {___, tmp[[2]], ___}];
Sow[tmp];
]];
out = out[[2, 1]];
left = Complement[Range[Length[pts]], Flatten[out]];
out = out~Join~Partition[left, 2];
out = TrySwitchAll[pts, out];
out
,
Print["Even number of points >=2 needed!"]
]
]
Which gives the same answer. Note that any good solution, that there are no lines crossing; for if there were crossing lines we could swap the points to get a smaller total. See also https://www.youtube.com/watch?v=GX3URhx6i2E around the 28:30... for a similar problem.