Message Boards Message Boards

[?] Get the FourierTransform of a two dimension door function?

Abdelkarim BOSKRI
Posted 8 years ago

Please did you can help me to make the foueeir transform of two dimension door function

FourierTransform[Piecewise[{{1, x^2 + y^2 <= 1}, {0, x^2 + y^2 > 1}}], {x, y}, {u, v}]

When i make the previous commande, i can't have anay result Thank you
POSTED BY: Abdelkarim BOSKRI
2 Replies
Sort By:

Hi Abdelkarim,

the Fourier transform of a rotational symmetric function is basically a Hankel transform. In the 2D case it is a Hankel transform of order 0. So here we simply can calculate:

HankelTransform[HeavisideTheta[1 - r], r, \[Rho]]

which gives an immediate result in terms of a Bessel function.

Regards -- Henrik

Edit:

@Michael Helmle : Sorry, I did not see your answer - which I prefer! I was thinking more in terms of mathematics than of Mathematica ...
POSTED BY: Henrik Schachner
Michael Helmle
Michael Helmle
Posted 8 years ago

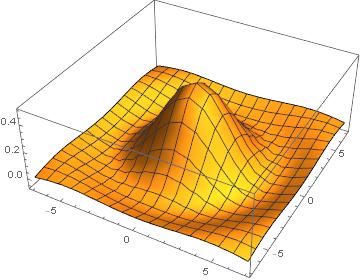
Your code works for me:

$Version

(* "11.1.0 for Microsoft Windows (64-bit) (March 13, 2017)"*)

f1 = FourierTransform[
  Piecewise[{{1, x^2 + y^2 <= 1}, {0, x^2 + y^2 > 1}}], {x, y}, {u, 
   v}] 

(* BesselJ[1,Sqrt[u^2+v^2]]/Sqrt[u^2+v^2]*)

Plot3D[f1, {u, -7, 7}, {v, -7, 7}, PlotRange -> All]

enter image description here
POSTED BY: Michael Helmle
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract