Mariusz Iwaniuk, thanks for help. I apologize for the mistake committed by me. I'm doing my first steps in Mathematica. I try to plot figure from function:

1-NIntegrate[Exp[-1/2*(y - Sqrt[2*ebn0*R])^2]*Log[2, Exp[-2*Sqrt[2*ebn0*R]*y] + 1], {y, -5, 20}, Method -> "LobattoKronrodRule"]/(Sqrt[2*Pi]*Log[2])) == R;

I need to plot ebn0(R), but I don't know how can I do this. This plot should be equivalent to Figure 4 : Capacity of the Binary-Input Channel.`

I had to remove $log(2)$ from the denominator from equation and I must to replace the expression $Eb/N0$ with $10^{\text{Eb/N0}/10}$ in order for the plot to be correct .

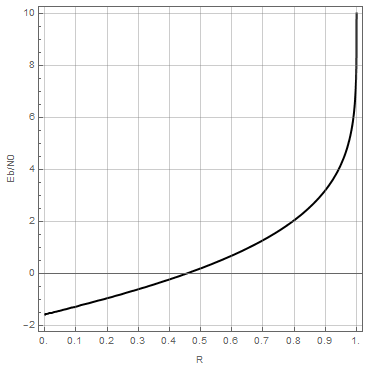
     Int2[R_?NumericQ, ebNo_?NumericQ] := NIntegrate[Exp[-1/2*(y - Sqrt[2*ebNo*R])^2] 
     Log[2, Exp[-2*Sqrt[2*ebNo*R]*y] + 1], {y, -Infinity, Infinity}, Method -> "LobattoKronrodRule"];

     ContourPlot[R == 1 - Int2[R, 10^(ebNo/10)]/Sqrt[2*Pi], {R, 0.001, 1}, {ebNo, -2, 10}, Axes -> True, 
     GridLines -> {Table[n, {n, 0, 1, 0.1}], Table[n, {n, -2, 10, 2}]}, ContourStyle -> {Black, Thick}, 
     FrameTicks -> {{All, None}, {Table[n, {n, 0, 1, 0.1}], None}}, FrameLabel -> {"R", "Eb/N0"}]

Have a nice day :)

You did a mistakes in $e^{\frac{1}{2} (y-b)^2}$,it should be:$e^{-\frac{1}{2} (y-b)^2}$

Int[b_?NumericQ] := NIntegrate[Exp[-1/2*(y - b)^2]*Log[2, Exp[-2*b*y] + 1], {y, -5, 20}, Method -> "LobattoKronrodRule"];
ListPlot[Table[{b, (1 - Int[b]/(Sqrt[2*Pi]*Log[2]))}, {b, -3, 3, 1/10}], Joined -> True,PlotLegends -> {"eq(b)"}] // Quiet

 FindRoot[(1 - Int[b]/(Sqrt[2*Pi]*Log[2])) == 0, {b, 7/10}, WorkingPrecision -> 20]
 (*{b -> 0.73171520950283916124}*)
 FindRoot[(1 - Int[b]/(Sqrt[2*Pi]*Log[2])) == 0, {b, -7/10}, WorkingPrecision -> 20]
 (*{b -> -0.73171520950283916124}*)

Next time give us a correct equation.

The Wolfram Language is case sensitive.