I found a new surprising approximation to the MRB constant. That got me wondering what surprising approximations you could come up with using Mathematica. The MRB constant is ![Sum[(-1)^n*(n^(1/n) - 1), {n, 1, Infinity}]](http://community.wolfram.com//c/portal/getImageAttachment?filename=40342.JPG&userId=366611) .
.
m = NSum[(-1)^n*(n^(1/n) - 1), {n, 1, Infinity},
Method -> "AlternatingSigns", WorkingPrecision -> 2000];
Here is an algorithm that gives over 38 digits per iteration using integer coefficients of an average of less than 38 digits.
![m = Sum[(x^(1/x)*p[x])/(E^(28<em>Pix) - 157329), {x, 1, Infinity}]](http://community.wolfram.com//c/portal/getImageAttachment?filename=931210.JPG&userId=366611)
where the p's come from the following.
p[0] = 1; Table[
t[n] = m - Sum[(x^(1/x)*p[x])/(E^(28*Pi*x) - 157329), {x, 1, n}] ;
p[n + 1] =
IntegerPart[
t[n]/((n + 1)^(1/(n + 1))/(-157329 + E^(28 (n + 1) Pi)))], {n, 0,
50}]; m - Sum[(x^(1/x)*p[x])/(E^(28*Pi*x) - 157329), {x, 1, 50}]
ListLinePlot[Table[p[x], {x, 50}]] .
This gives 4.43245253327023142515697487229517050305562747970
3516515309207411311257382068818424053632*10^-1911
and
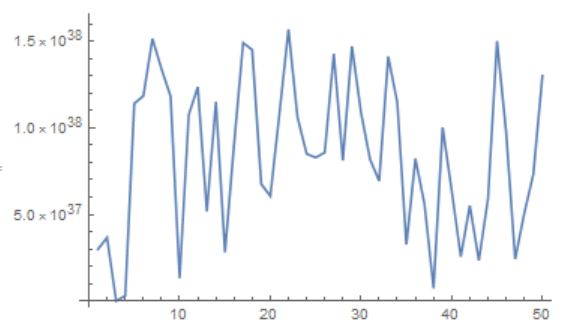
How about you?