Goal of the Project
 (from: http://blog.stephenwolfram.com/2016/05/solomon-golomb-19322016/)
(from: http://blog.stephenwolfram.com/2016/05/solomon-golomb-19322016/)
What happens in feedback shift register is that in each step, all values shift one position to the left and one new number, either 0 or 1, is added at the very right side by taking numbers from the given tap positions and operating some function between them in modulo 2.
Linear Feedback Shift Registers (LFSRs), which use linear function to produce new numbers, have long been used to produce random sequences/numbers for various technologies such as USB, Wi-Fi, and 3G networks. In fact, it is estimated that in applications, the algorithm for LFSRs has been run more than octillion times. However, there have been few studies on nonlinear feedback shift registers. The main goal of my project was to find a combination of taps and nonlinear function that produces a random sequence for a feedback shift register (i.e. the sequence passes randomness tests).
Summary of Work
Throughout the summer school, I have formulated functions to test whether certain combinations of tap positions and nonlinear function produce the sequence of maximal length, which is length 2^n-1 (n is the length of the shift register). This is because there are only there are 2^n possible states and the sequence of all 0s cannot evolve to any new state. I tested all NFSRs with 2 taps and 3 taps for n<16, and all NFSRs with 4 taps for n<10. (Some notable nonlinear feedback functions were further tested with bigger length). I then ran several statistical randomness tests such as the equidistribution test, the serial test, and the poker test, to identify combinations that produce random sequences. I also made some analyses of the tap positions and nonlinear functions that produce long random sequences. The following function give the list of 3-tap nonlinear feedback shift registers that produce sequences of maximal length.
{x, y, z} : {3, 2, 1} (descending order)
nfsr3[a_]:=
(nonlinear[taps_]:=
(taps ;
k[x_] :=Values[Counts[Partition[ShiftRegisterSequence[{a,taps,#/.AssociationThread[Tuples[{0,1},3]-> x]&}],a,1]]];
maxseqgen:= Select[Tuples[{0,1},8],k[#] == PadLeft[{},(2^a)-a,1]&];
m = {{1,1,1,1,1,1,1,1},{0,1,0,1,0,1,0,1},{0,0,1,1,0,0,1,1},{0,0,0,0,1,1,1,1},{0,0,0,1,0,0,0,1},{0,0,0,0,0,0,1,1},{0,0,0,0,0,1,0,1},{0,0,0,0,0,0,0,1}};
nonlinearcasefeed:=Flatten[Mod[#.m,2]&/@(Cases[Values[Solve[{n,x,y,z,xy,yz,zx,xyz}.m == #,{n,x,y,z,xy,yz,zx,xyz},Modulus->2]&/@(maxseqgen)],Except[{{_,_,_,_,0,0,0,0}}]]),1];
fxninm:=(Flatten[Values[Solve[{n,x,y,z,xy,yz,zx,xyz}.m == #,{n,x,y,z,xy,yz,zx,xyz},Modulus->2]&/@(nonlinearcasefeed)],1]);
{{taps,(fxninm[[#]][[1]]*1+fxninm[[#]][[2]]*x+fxninm[[#]][[3]]*y+fxninm[[#]][[4]]*z+fxninm[[#]][[5]]*xy+fxninm[[#]][[6]]*yz+fxninm[[#]][[7]]*zx+fxninm[[#]][[8]]*xyz)&/@Range[Length[Flatten[Values[Solve[{n,x,y,z,xy,yz,zx,xyz}.m == #,{n,x,y,z,xy,yz,zx,xyz},Modulus->2]&/@(nonlinearcasefeed)],1]]]}});
Flatten[nonlinear/@Select[Permutations[Range[a],{3}],OrderedQ],1]);
k is the function that gives the list of 1s when the sequence does not have any overlap. In other words, the ones with all 1s are the maximal length sequences. I have tested all functions and selected the ones that give the list of 1s using maxseqgen. I then used dot product of the matrix to find the polynomial shape of each maximal length-generating function and selected only the nonlinear functions using nonlinearcasefeed. I have tested all possible configurations of taps for a given length a. The following are the results for cases length a=3 to 8.
The following are some of the results I got from running the function above:
nfsr3[7]
{{{1, 2, 3}, {1 + x + xy + z, 1 + xy + y + z}}, {{1, 2, 4}, {}}, {{1, 2, 5}, {}}, {{1, 2, 6}, {x + xy + y + z, 1 + xy + z}},
{{1, 2, 7}, {}}, {{1, 3, 4}, {}}, {{1, 3, 5}, {}}, {{1, 3, 6}, {}}, {{1, 3, 7}, {x + xy + y + z, 1 + xy + z}}, {{1, 4, 5}, {}},
{{1, 4, 6}, {}}, {{1, 4, 7}, {}}, {{1, 5, 6}, {}}, {{1, 5, 7}, {}}, {{1, 6, 7}, {1 + x + xy + z, 1 + xy + y + z}},
{{2, 3, 4}, {}}, {{2, 3, 5}, {}}, {{2, 3, 6}, {}}, {{2, 3, 7}, {}}, {{2, 4, 5}, {}}, {{2, 4, 6}, {}}, {{2, 4, 7}, {}},
{{2, 5, 6}, {}}, {{2, 5, 7}, {}}, {{2, 6, 7}, {}}, {{3, 4, 5}, {}}, {{3, 4, 6}, {}}, {{3, 4, 7}, {}}, {{3, 5, 6}, {}},
{{3, 5, 7}, {}}, {{3, 6, 7}, {}}, {{4, 5, 6}, {}}, {{4, 5, 7}, {}}, {{4, 6, 7}, {}}, {{5, 6, 7}, {}}}
nfsr3[8]
{{{1, 2, 3}, {}}, {{1, 2, 4}, {}}, {{1, 2, 5}, {}}, {{1, 2, 6}, {x + xy + y + z, 1 + xy + z}}, {{1, 2, 7}, {}},
{{1, 2, 8}, {}}, {{1, 3, 4}, {}}, {{1, 3, 5}, {}}, {{1, 3, 6}, {}}, {{1, 3, 7}, {}}, {{1, 3, 8}, {}},
{{1, 4, 5}, {x + xy + y + z, 1 + xy + z}}, {{1, 4, 6}, {}}, {{1, 4, 7}, {}}, {{1, 4, 8}, {x + xy + y + z, 1 + xy + z}},
{{1, 5, 6}, {x + xy + y + z, 1 + xy + z}}, {{1, 5, 7}, {}}, {{1, 5, 8}, {}}, {{1, 6, 7}, {}}, {{1, 6, 8}, {}}, {{1, 7, 8}, {}},
{{2, 3, 4}, {}}, {{2, 3, 5}, {}}, {{2, 3, 6}, {}}, {{2, 3, 7}, {}}, {{2, 3, 8}, {}}, {{2, 4, 5}, {}}, {{2, 4, 6}, {}},
{{2, 4, 7}, {}}, {{2, 4, 8}, {}}, {{2, 5, 6}, {}}, {{2, 5, 7}, {}}, {{2, 5, 8}, {}}, {{2, 6, 7}, {}}, {{2, 6, 8}, {}},
{{2, 7, 8}, {}}, {{3, 4, 5}, {}}, {{3, 4, 6}, {}}, {{3, 4, 7}, {}}, {{3, 4, 8}, {}}, {{3, 5, 6}, {}}, {{3, 5, 7}, {}},
{{3, 5, 8}, {}}, {{3, 6, 7}, {}}, {{3, 6, 8}, {}}, {{3, 7, 8}, {}}, {{4, 5, 6}, {}}, {{4, 5, 7}, {}}, {{4, 5, 8}, {}},
{{4, 6, 7}, {}}, {{4, 6, 8}, {}}, {{4, 7, 8}, {}}, {{5, 6, 7}, {}}, {{5, 6, 8}, {}}, {{5, 7, 8}, {}}, {{6, 7, 8}, {}}}
I have also made similar function for NFSRs with 4 taps (slight modifications from 3-tap NFSR function were made based on the possible feedback functions.
{x, y, z, w} : {4, 3, 2, 1} (descending order)
nfsr4[a_]:=
(nonlinear[taps_]:=
(taps ;
k[x_] :=Values[Counts[Partition[ShiftRegisterSequence[{a,taps,#/.AssociationThread[Tuples[{0,1},4]-> x]&}],a,1]]];
maxseqgen:= Select[Tuples[{0,1},16],k[#] == PadLeft[{},(2^a)-a,1]&];
m = {{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},{0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1},{0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1},{0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1},{0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1},{0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1},{0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,1},{0,0,0,0,0,0,0,0,0,1,0,1,0,1,0,1},{0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,1},{0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1},{0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1},{0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1},{0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1},{0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1},{0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1},{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1}};
nonlinearcasefeed:= Flatten[Mod[#.m,2]&/@(Cases[Values[Solve[{n,x,y,z,w,xy,xz,xw,yz,yw,zw,xyz,xyw,xzw,yzw,xyzw}.m == #,{n,x,y,z,w,xy,xz,xw,yz,yw,zw,xyz,xyw,xzw,yzw,xyzw},Modulus->2]&/@(maxseqgen)],Except[{{_,_,_,_,_,0,0,0,0,0,0,0,0,0,0,0}}]]),1];
cases[feed_]:=
{taps,Flatten[(#[[1]]*1+#[[2]]*x+#[[3]]*y+#[[4]]*z+#[[5]]*w+#[[6]]*xy+#[[7]]*xz+#[[8]]*xw+#[[9]]*yz+#[[10]]*yw+#[[11]]*zw+#[[12]]*xyz+#[[13]]*xyw+#[[14]]*xzw+#[[15]]*yzw+#[[16]]*xyzw)&/@Values[Solve[{n,x,y,z,w,xy,xz,xw,yz,yw,zw,xyz,xyw,xzw,yzw,xyzw}.m == #,{n,x,y,z,w,xy,xz,xw,yz,yw,zw,xyz,xyw,xzw,yzw,xyzw},Modulus->2]]&/@{feed},1]};
cases/@nonlinearcasefeed);
Flatten[nonlinear/@Select[Permutations[Range[a],{4}],OrderedQ],1]);
https://github.com/sy375/sy375/tree/master/Cases
The cases for 2 taps, the statistical randomness tests (frequency test, serial test, and poker test), visualization of random cases, and several other notable cases (e.g. sol case) are included in the GitHub link above.
Main Results
As the main goal of my project was to find NFSRs that produce long random sequences, these are some of the settings of NFSRs (taps positions and length n) that produced such sequences: Main Results in Detail
The following are the 3-tap NFSRs of n<16 that passed frequency test, serial test, and poker tests for triples, quadruples, and quintuples at p=25%:
3 taps
{x, y, z} : {3, 2, 1} (descending order)
n=12; {{1,5,8},{x+y+z+xy}},{{1,5,8},{1+xy+z}}
n=8; {{1,2,6},{x+y+z+xy}}, {{1,5,6},{1+xy+z}}
n=7; {{1,2,6},{x+y+z+xy}}, {{1,3,7},{x+y+z+xy}}, {{1,3,7},{1+xy+z}}
n=6; {{1,3,6},{1+xy+z}}
The following are some of the 4-tap NFSRs that passed frequency test, serial test, and poker test for triples at p=25%:
4 taps
{x, y, z, w} : {4, 3, 2, 1} (descending order)
n=16; {{1,5,8,10},{1+w+x+xyz+xz+y+yz}}, {{1,5,8,10},{w+x+xy+xyz+y+z}}, ...
n=15; {{1,2,4,6},{1+w+xy+yz}}, {{1,11,13,15},{1+w+x+xy+yz+z}}, ...
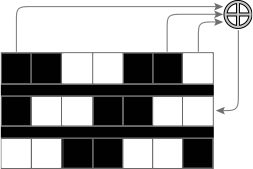
The randomness can be observed by visualizing such cases into white and black for 0 and 1 correspondingly:
Image[Partition[ShiftRegisterSequence[{12, {1, 5, 8}, Mod[#[[1]] + #[[2]] + #[[3]] + #[[3]]*#[[2]], 2] &}], 16]]

Image[Partition[ShiftRegisterSequence[{12, {1, 5, 8}, Mod1 + #[[1]] + #[[3]]*#[[2]], 2] &}], 16]]

Image[Partition[ShiftRegisterSequence[{16, {1, 5, 8, 10}, Mod[#[[1]] + #[[4]] + #[[4]]*#[[3]]*#[[2]] + #[[4]]*#[[3]] + #[[3]] + #[[2]], 2] &}], 16]]

Partition[ShiftRegisterSequence[{16, {1, 5, 8, 10}, Mod[1 + #[[1]] + #[[4]] + #[[4]]*#[[3]]*#[[2]] + #[[4]]*#[[2]] + #[[3]] + #[[2]]*#[[3]], 2] &}], 16]

Conclusions
For nonlinear shift registers with 3 taps and of length smaller than 16, there were 8 cases in which the sequence passed all randomness tests of confidence level 25 %. The following are the list of cases : n = 12; {{1, 5, 8}, {x + y + xy + z}}, {{1, 5, 8}, {1 + xy + z}}, n = 8; {{1, 2, 6}, {x + y + xy + z}}, {{1, 5, 6}, {1 + xy + z}}, n = 7; {{1, 2, 6}, {x + y + xy + z}}, {{1, 3, 7}, {x + y + xy + z}}, {{1, 3, 7}, {1 + xy + z}}, and n = 6; {{1, 3, 6}, {1 + xy + z}}. Compared to the sequences produced by LFSRs, these sequences seem to produce fairly nice random numbers.
In addition, I could observe four big features for the settings of NFSRs (tap positions and nonlinear functions) that produced sequences of maximal length :
First, tap1 was always included, no matter the number of taps nor the length of shift register. For 2 - tap NFSRs, I have tested length n from 3 to 16 and only length 3 shift registers were observed, which had tap configuration {1, 2} and {1, 3}. For 3 - tap NFSRs, I have tested all the cases for length n from 3 to 15, and although there were a lot of cases, the maximal - sequence generating NFSRs all had tap1 as one of the tap positions. For 4 - tap NFSRs, I have tested cases for length n from 4 to 9 as well as some notable functions such as sol case (w + x + y + yz + xy + xz), reverse of sol case (1 + w + x + y + yz + xy + xz), and w + x + xy + xyz + y + z, and all these cases had tap1 as one of 4 taps.
Second, the cases seem to decrease as the length of the shift registers increased. For 2 - tap NFSRs, 3 combinations produced maximum - length sequences when n = 3 and no other combination was available for n < 17. For 3 - tap NFSRs, the number of combinations decreased from n = 3 (47 cases) to n = 8 (8 cases), no case for n = 9, 10, 11, 4 cases for n = 12, and no case for n = 13, 14, 15. For 4 - tap NFSRs, the number of combinations seem to decrease from n = 4 to n = 9, and there seem to be fewer cases for bigger shift register. This should be further studied to find whether there is certain limit on the length of NFSR for a given number of taps.
Third, the feedback function seem to have the shape f(tap2, ..., tapk) + tap1 (e.g. f(tap2, tap3) + tap1 for 3 - tap NFSRs and f(tap2, tap3, tap4) + tap1 for 4 - tap NFSRs), meaning that tap1 was independent from the nonlinear part of the function. Such pattern is valid in every NFSR of taps more than 2 for all the ones I have tested. This should also be further tested to see whether the nonlinear feedback function has the shape f(tap2, ..., tapk) + tap1 for any positive integer k > 2.
Fourth, for the cases of 3 - tap NFSRs, the two most common nonlinear function were x + y + xy + z and 1 + xy + z (these functions produced sequence of maximal length when n =3,4,5,6,7,8,12), which are rule 30 and the complement of rule 30 (rule 135) when translated into the rule numbering system of elementary cellular automata. This is interesting in that rule 30, which is one of the most widely used and unique elementary Cellular Automaton, is the best random sequence generating rule. We say that these two functions appear as a pair because, for a given choice of tap positions and length n, each function produces a sequence of maximal length if and only if the other function produces a sequence of maximal length. In addition, the next two common functions that appeared were 1 + z + x + xy and 1 + z + y + xy (these functions produced sequence of maximal length when n =3,4,5,6,7). These are actually rule 45 and the complement of rule 45 (rule 75), which are also unique elementary cellular automata rules (Class 3). We should also be aware how those complementary rules acted somewhat similarly in producing maximum - length NFSRs. Such pairwise pattern is also observable in 4 - tap NFSRs (e.g. 1 + w + x + xyz + xz + y and 1 + w + x + xy + xyz + yz are pairs), but further analysis on the relationships between the pairs is needed.
Future Directions
For future work, 4-tap NFSRs should be tested for bigger shift registers and NFSRs with more taps should also be tested in order to figure out whether the shape f(tap2, ..., tapk) + tap1 can be generalized for all nonlinear feedback functions with more than 2 taps. There should also be analysis on pair-appearing functions for 4-tap NFSRs. In order to do such further analysis, the function I made for 4 taps should first be tested on bigger n. Because it took 27 hours to operate the function for n=9, it is likely that it will take very long time to run the function for bigger length. After the operation, the nonlinear feedback function should be analyzed in comparison with k=2, r=3/2 cellular automata to figure out how the pairwise functions are related.
Background Info/References
http://blog.stephenwolfram.com/2016/05/solomon-golomb-19322016/
http://www.wolframscience.com/nks/notes-7-5--random-number-generators/
http://www.wolframscience.com/nks/notes-10-10--nonlinear-feedback-shift-registers/
http://www.wolframscience.com/nks/notes-10-9--tests-of-randomness/
Knuth, Donald. The Art of Computer Programming Volume 2: Seminumerical Algorithms. Upper Saddle River, NJ: Addison-Wesley.
Key Words: Feedback Shift Register, Random Number Generator (RNG), Computational Universe
 Attachments:
Attachments: