Questions regarding neural networks

The recent overwhelming success of neural networks in machine learning has inspired the investigation of their internal processes in an attempt to understand "how, and exactly what, the network learns". However, neural networks are still widely considered "black boxes", mysterious even to those who are experts in building them. This is largely because despite the relative straightforwardness in understanding of the overall construction of neural networks at an architectural level, the actual manipulation of data occurs in such high-dimensional spaces that the sheer complexity and volume of information contained inside a network goes beyond human cognitive capacities.

However, even if we cannot observe each individual training example progress through its transformations within a network, this is not to say that the internal processes in networks are impenetrable. Indeed, observing the weights learned by a neural network at different stages of its training gives insight into what is learned over the course of training, how what is learned changes, and the responsibilities of different layers on overall learning.

LeNet

LeNet, first introduced by LeCun et al. in their 1998 paper Gradient-Based Learning Applied to Document Recognition, has demonstrated considerable success in character and digit recognition. It's also simple, making it a nice architecture to study for interpretability.

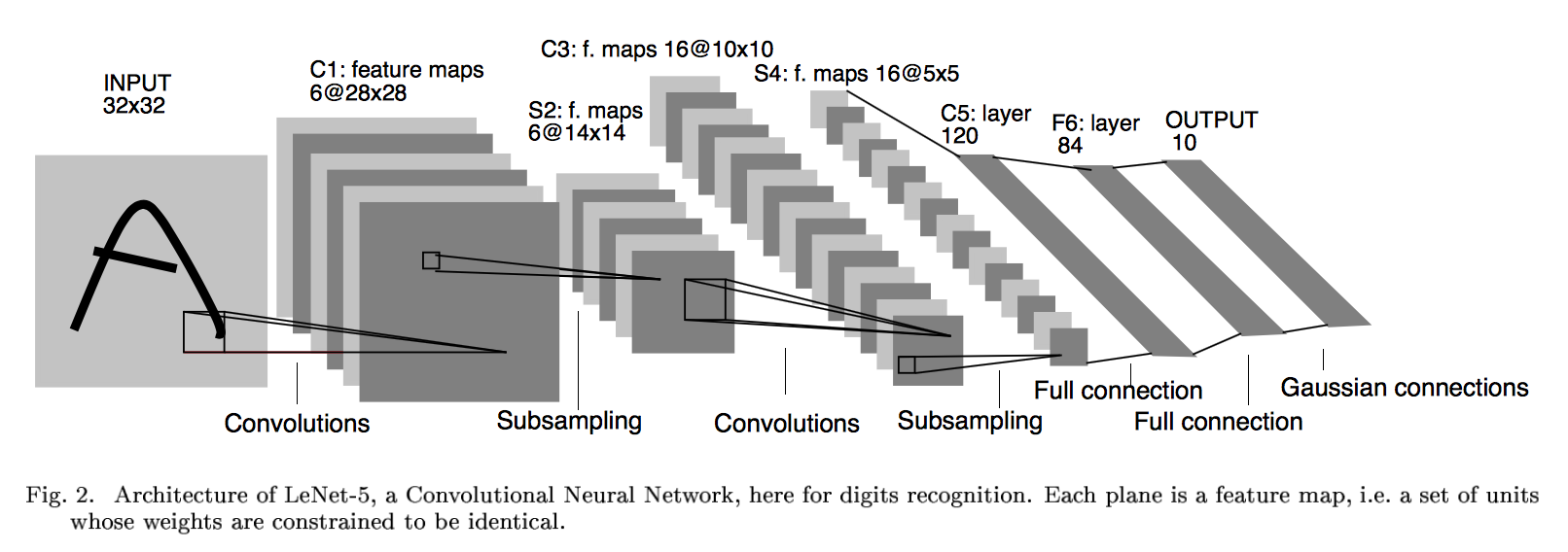
It's straightforward to use the WL neural network package to implement LeNet.

lenet = NetChain[{
           ConvolutionLayer[20, 5],
           Ramp,
           PoolingLayer[2, 2],
           ConvolutionLayer[50, 5],
           Ramp, 
           PoolingLayer[2, 2],
           FlattenLayer[],
           500,
           Ramp,
           10,
           SoftmaxLayer[]
        },
     "Output" -> NetDecoder[{"Class", Range[0, 9]}],
     "Input" -> NetEncoder[{"Image", {28, 28}, "Grayscale"}]
    ]

And moreover, in Mathematica 11.1, you can use NetModel to call a LeNet pre-trained on MNIST data.

NetModel["LeNet Trained on MNIST Data"]

Visualizing filters over the course of training

We can get a sense of what LeNet is "learning" by observing how the weights at various layers change as the network trains. Naturally, we can visualize these as sets of images. We can use WL's Image function to this end, using colors to indicate weight magnitude. Here, red indicates strongly positive values, blue indicates strongly negative values, and green values hover around 0.

MNIST

Layer 1: 1st convolutional layer

LeNet's first convolutional layer learns 20 5x5 filters. A random initialization of the network yields the following 1st-layer filters:

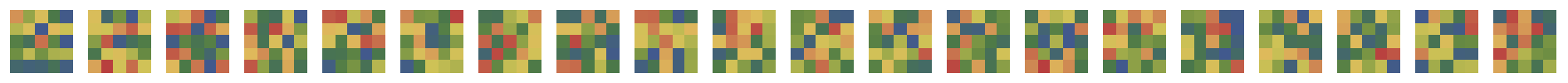
In a network that is learning, we expect the filters to change over the course of training. Taking snapshots of the filters at regular intervals as training progresses, however, reveals that these filters change little, if at all. Indeed, at least to the human eye, they seem to change not at all over 29 training epochs.

Indeed though this does make for quite the pretty tiling, it does make for a dissatisfying image of filter learning.

Studying the weights at regular intervals over the training process of LeNet on MNIST revealed that the convolutional filters undergo little to no change over the course of training. Indeed, freezing the convolutional layers (preventing their weights from changing after their initial random initialization) in LeNet results in an accuracy loss of approx. 4% on an identically initialized, unfrozen net with accuracy 96%. That is, freezing the convolutional layers on a network that would have otherwise achieved 96% accuracy reduces the accuracy to 92%.

This suggests that most of the information discriminating between digits can be captured in the linear layers, and thus that the MNIST dataset is so structurally simple that it can be effectively learned with logistic regression.

The CIFAR-10 dataset, however, is apparently substantially more complex. Here, the filters do show signs of learning-- that is, their weights do change substantially over the course of training. Moreover, freezing the convolutional layers reduces accuracy dramatically, from an unfrozen accuracy of 69.68% to 55.65%, approximately a 20% reduction in accuracy.

Visualization of filters

(coming soon)