GOAL OF THE PROJECT:
The goal of the project is to understand what kind of ground states are realized for a generalized Ising model with a given set of energy weights.
SUMMARY OF WORK:
- Starting from random distributions states with local minimal energy were obtained via Monte Carlo (MC) and Cellular automaton (CA) techniques.
- Exhaustive search for small field sizes was done.
The 2 D Ising model is a system of interacting spins placed in the integer points of a rectangular grid. The energy of the system s is given by the list convolution of the weight pattern and the list of spin values s
e[s_, patternNum_] := Apply[Plus, s ListConvolve[pattern, s, 2], {0, 1}]
The weight pattern is defined as
pattern = 1/2{{ w4,w1,w3},{w2,0,w2},{w3,w1,w4}}
and the values for w's span {-2,-1,0,1,2}.
Monte Carlo
One can implement MC choosing a spin randomly and flipping it if it reduces the energy (Metropolis algorithm). To speed up one may choose a random spin within a square which is m times less than the whole field and m-periodically construct its copies to span the whole field. Then one calculates energy shifts from the (m/n)^2 spin-flips and flips only those which decrease the energy.
ClearAll[n, field, m, w1, w2, w3, w4, \[CapitalDelta]e1, position, positions, op];
n = 2^6; field = RandomInteger[1, {n, n}] /. 0 -> -1; w1 = 2; w2 = 2; w3 = 0; w4 = 0;
\[CapitalDelta]e1 = position \[Function] ((field[[Mod[#1 - 1, n, 1], Mod[#2 + 1, n, 1]]]
+ field[[Mod[#1 + 1, n, 1], Mod[#2 - 1, n, 1]]]) w4
+ (field[[Mod[#1 - 1, n, 1], Mod[#2 - 1, n, 1]]]
+ field[[Mod[#1 + 1, n, 1], Mod[#2 + 1, n, 1]]]) w3
+ (field[[Mod[#1 - 1, n, 1], #2]] + field[[Mod[#1 + 1, n, 1], #2]])w1
+ (field[[#1, Mod[#2 - 1, n, 1]]] + field[[#1, Mod[#2 + 1, n, 1]]])w2 ) field[[#1, #2]] &[Sequence @@ position];
positions[m_] := With[{position = RandomInteger[{1, n/m}, 2]},
If[Or @@ Flatten@Table[If[\[CapitalDelta]e1[{#1, #2}] > 0, field[[#1, #2]] *= -1; True, False] &
[Mod[position[[1]] + n/m i, n, 1], Mod[position[[2]] + n/m j, n, 1]], {i, 0, m - 1}, {j, 0, m - 1}], Sow[field]]]
Monitor[op = Reap[Do[positions[16], {monitor, 1, 500}]][[2]];//AbsoluteTiming, monitor]
Tooltip[ArrayPlot[field /. -1 -> 0, PixelConstrained -> 2], "{2,2,0,0}"]
Manipulate[ArrayPlot[op[[1, l]] /. -1 -> 0, PixelConstrained -> 2], {l,1,Length[op[[1]]], 1}, SaveDefinitions -> True]
Cellular Automata
One may build a cellular automaton locally reducing (not increasing) energy at each step. To this end one builds a rule based on the pattern
ClearAll[patterns]
stepNumber = 20; n = 2^6; field = RandomInteger[1, {n, n}] /. 0 -> -1;
patterns = {{{0, 1, 0},{1, 0, 1},{0, 1, 0}}, -{{0, 1, 0},{1, 0, 1},{0, 1, 0}}, {{0, 1, 0},{2, 0, 2},{0, 1, 0}},
-{{0, 1, 0},{2, 0, 2},{0, 1, 0}}, {{0, 1, 0},{-1, 0, -1},{0, 1, 0}}, {{0, 1, 0},{-2, 0, -2},{0, 1, 0}},
-{{0, 1, 0},{-2, 0, -2},{0, 1, 0}}, {{0, 1, 0},{0, 0, 0},{0, 1, 0}}, -{{0, 1, 0},{0, 0, 0},{0, 1, 0}}};
DecreaseEnergy[matrix_, pattern_] := If[matrix[[2, 2]] Plus @@ Flatten[matrix pattern] > 0, -matrix[[2, 2]], matrix[[2, 2]]]
DecreaseEnergy1[matrix_, pattern_] := If[matrix[[2, 2]] Plus @@ Flatten[matrix pattern] >= 0, -matrix[[2, 2]], matrix[[2, 2]]]
tuin = Tuples[{-1, 1}, {3, 3}];
In fact one can build two rules based on the decision to flip or not to flip if the energy does not change.
tuout = Table[Thread[tuin -> (DecreaseEnergy[#, patterns[[i]]] & /@ tuin)] /. -1 -> 0, {i, 1, Length[patterns]}];
tuout1 = Table[Thread[tuin -> (DecreaseEnergy1[#, patterns[[i]]] & /@ tuin)] /. -1 -> 0, {i, 1, Length[patterns]}];
rule[matrix_, a_, ruleNumber_] := matrix /. tuout[[ruleNumber]]
rule1[matrix_, a_, ruleNumber_] := matrix /. tuout1[[ruleNumber]]
caFunction0[ruleN_] := CellularAutomaton[{rule[#1, #2, ruleN] &, {}, {1, 1}}, RandomInteger[1, {n, n}], stepNumber];
caFunction1[ruleN_] := CellularAutomaton[{rule1[#1, #2, ruleN] &, {}, {1, 1}}, RandomInteger[1, {n, n}], stepNumber];
evolution = caFunction0 /@ Range[Length[patterns]];
evolution1 = caFunction1 /@ Range[Length[patterns]];
e[s_, patternNum_] := Apply[Plus, s ListConvolve[patterns[[patternNum]], s, 2], {0, 1}]
allenergies = Table[e[evolution[[j, i]], j], {j, 1, Length[patterns]}, {i, 1, stepNumber}];
Manipulate[Grid[Partition[Row[{
ArrayPlot[evolution[[#, i]], PixelConstrained -> 2, PlotLabel -> "E = " <> ToString[allenergies[[#, i]]]], Spacer[3],
ListPlot[{allenergies[[#]], {{i, allenergies[[#, i]]}}}, PlotRange -> All, ImageSize -> 200, PlotStyle -> PointSize[Large],
AxesLabel -> {"Step"}]}] & /@ Range[Length[patterns]], 3], Frame -> All], {i, 1, stepNumber, 1},SaveDefinitions -> True]
allenergies1 = Table[e[evolution1[[j, i]], j], {j, 1, Length[patterns]}, {i, 1, stepNumber}];
Manipulate[ Grid[Partition[Row[{ArrayPlot[evolution1[[#, i]], PixelConstrained -> 2,
PlotLabel -> "E = " <> ToString[allenergies1[[#, i]]]], Spacer[3], ListPlot[{allenergies1[[#]],
{{i, allenergies1[[#, i]]}}}, PlotRange -> All, ImageSize -> 200, PlotStyle -> PointSize[Large]]}] & /@
Range[Length[patterns]],3], Frame -> All], {i, 1, stepNumber, 1}, SaveDefinitions -> True]
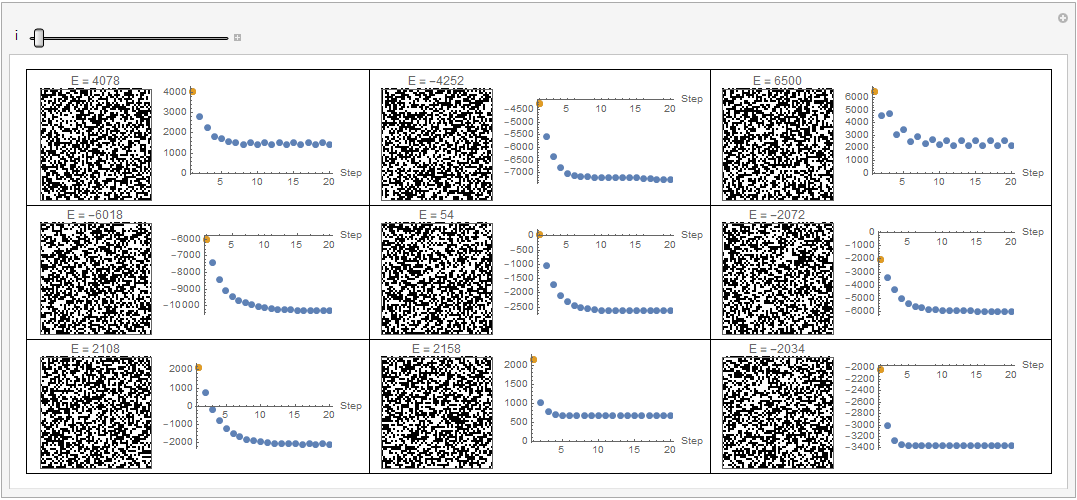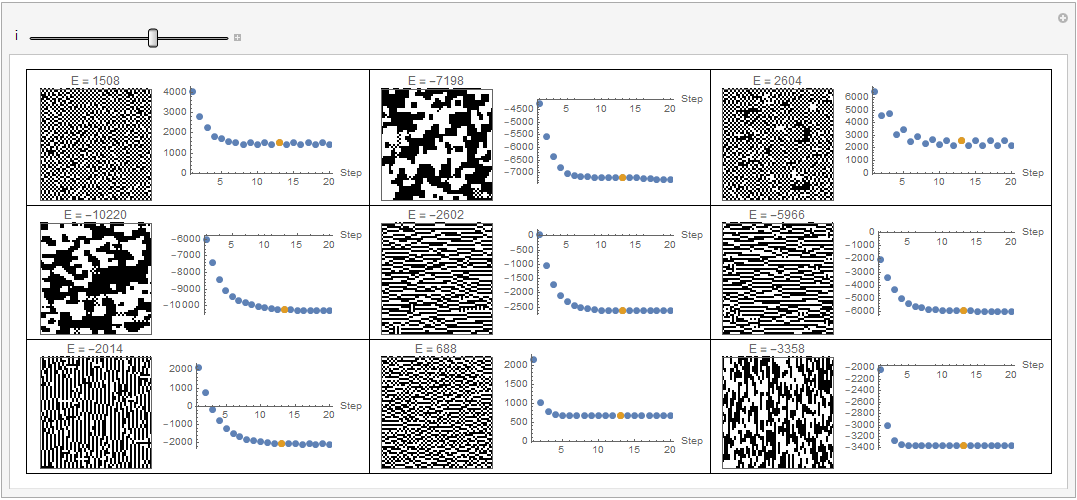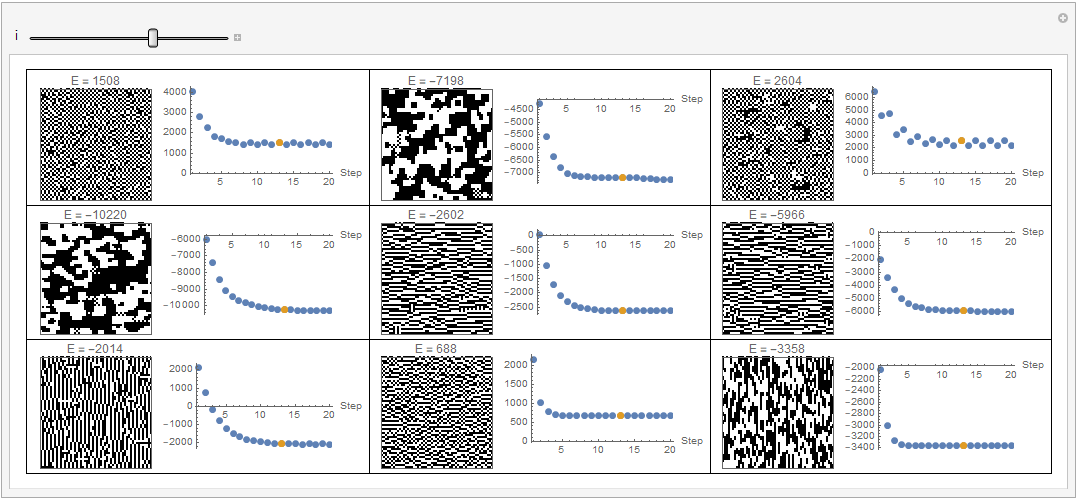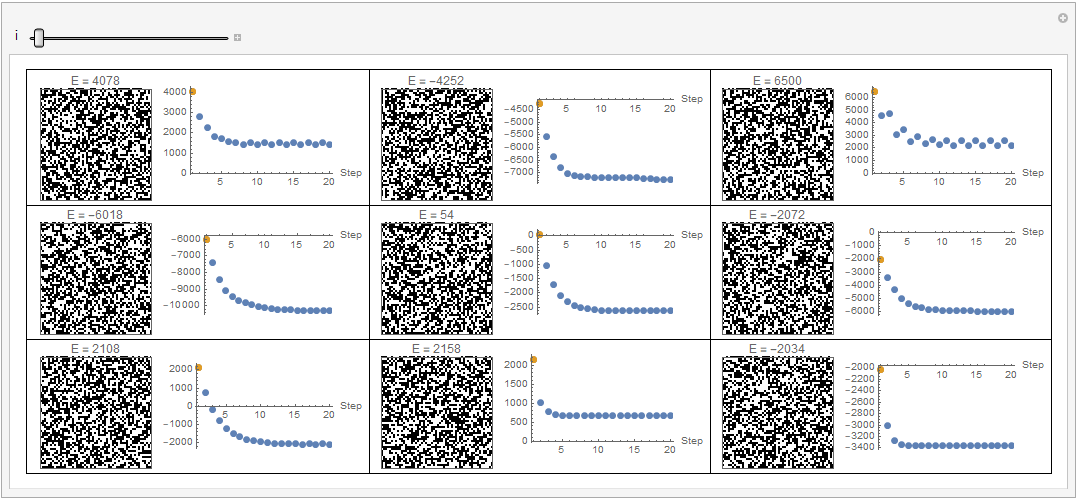
However the second rule - to flip is pathological and increases the energy globally.
One can also find out the number of the cellular automaton built. It is the binary code of the rule in the reverse order
rulNum = FromDigits[Reverse@tuout[[1, All, -1]], 2]
and draw the CA rules
RulePlot[CellularAutomaton[{rulNum, 2, {1, 1}}], Appearance -> "Simplified"]
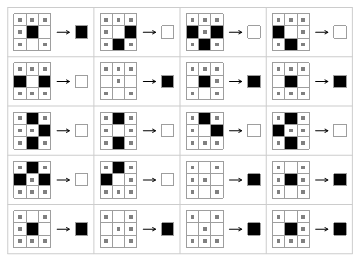
Here the dots mean any color.
Exhaustive search 3x3 field
Since there are just 2^9 possible configurations one can build them all at once and calculate their energy
patterns = {{{0, 1, 0},{1, 0, 1},{0, 1, 0}}, -{{0, 1, 0},{1, 0, 1},{0, 1, 0}},{{0, 1, 0},{2, 0, 2},{0, 1, 0}},
-{{0, 1, 0},{2, 0, 2},{0, 1, 0}},{{0, 1, 0},{-1, 0, -1},{0, 1, 0}}, {{0, 1, 0},{-2, 0, -2},{0, 1, 0}}),
-{{0, 1, 0},{-2, 0, -2},{0, 1, 0}}, {{0, 1, 0},{0, 0, 0},{0, 1, 0}},-{{0, 1, 0},{0, 0, 0},{0, 1, 0}}};
lattice = Tuples[{-1, 1}, {#, #}] &[3];
e[s_, patternNum_] := Apply[Plus, s ListConvolve[patterns[[patternNum]], s, 2], {0, 1}]
To take into account periodic boundary conditions and the symmety with respect to the flip of all spins, one has to exclude extra configurations
factorOutRotations[minE1_, size_] := Block[{minE = minE1, n = 1}, While[n < Length[minE],
With[{equivalentsets = Table[RotateLeft[RotateLeft[Partition[IntegerDigits[minE[[n]], 2, size^2]
, size], k]\[Transpose], j]\[Transpose], {k, 0, size - 1}, {j, 0, size - 1}]},
minE = Cases[minE,Except[Alternatives @@ Rest@Union@Flatten@Map[FromDigits[Flatten[#], 2] &,
Join[equivalentsets, equivalentsets /. {0 -> 1, 1 -> 0}], {2}]]]]; n++;]; minE]
exhausiveEnergies = Table[e[#, j] & /@ lattice, {j, 1, Length[patterns]}];
minEnergies = Min /@ exhausiveEnergies
energyMinimumPositions = MapThread[Position][{exhausiveEnergies, minEnergies}];
res4 = Map[FromDigits[Flatten[lattice[[#]] /. -1 -> 0], 2] &, energyMinimumPositions, {3}];
groundState = factorOutRotations[#, 3] & /@ (Flatten[res4, {3}][[1]])
Row /@ Map[ArrayPlot[Partition[IntegerDigits[#, 2, 9], 3], PixelConstrained -> 10] &, groundState, {2}]

For bigger fields one can implement sequential algorithm
energyCompiled5 =
Compile[{{fieldN, _Integer}, {w1, _Integer}, {w2, _Integer}, {w3, _Integer}, {w4, _Integer}},
Block[{d = Partition[N[IntegerDigits[fieldN, 2, 25]] /. 0. -> -1., 5]},
w3 (d[[1, 2]] d[[2, 1]] + d[[3, 5]] d[[2, 1]] +
d[[1, 3]] d[[2, 2]] + d[[1, 4]] d[[2, 3]] +
d[[1, 5]] d[[2, 4]] + d[[1, 1]] d[[2, 5]] +
d[[2, 2]] d[[3, 1]] + d[[2, 3]] d[[3, 2]] +
d[[2, 4]] d[[3, 3]] + d[[2, 5]] d[[3, 4]] +
d[[3, 2]] d[[4, 1]] + d[[3, 3]] d[[4, 2]] +
d[[3, 4]] d[[4, 3]] + d[[3, 5]] d[[4, 4]] +
d[[3, 1]] d[[4, 5]] + d[[1, 5]] d[[5, 1]] +
d[[4, 2]] d[[5, 1]] + d[[1, 1]] d[[5, 2]] +
d[[4, 3]] d[[5, 2]] + d[[1, 2]] d[[5, 3]] +
d[[4, 4]] d[[5, 3]] + d[[1, 3]] d[[5, 4]] +
d[[4, 5]] d[[5, 4]] + d[[1, 4]] d[[5, 5]] +
d[[4, 1]] d[[5, 5]]) +
w4 (d[[1, 5]] d[[2, 1]] + d[[3, 2]] d[[2, 1]] +
d[[1, 1]] d[[2, 2]] + d[[1, 2]] d[[2, 3]] +
d[[1, 3]] d[[2, 4]] + d[[1, 4]] d[[2, 5]] +
d[[2, 5]] d[[3, 1]] + d[[2, 2]] d[[3, 3]] +
d[[2, 3]] d[[3, 4]] + d[[2, 4]] d[[3, 5]] +
d[[3, 5]] d[[4, 1]] + d[[3, 1]] d[[4, 2]] +
d[[3, 2]] d[[4, 3]] + d[[3, 3]] d[[4, 4]] +
d[[3, 4]] d[[4, 5]] + d[[1, 2]] d[[5, 1]] +
d[[4, 5]] d[[5, 1]] + d[[1, 3]] d[[5, 2]] +
d[[4, 1]] d[[5, 2]] + d[[1, 4]] d[[5, 3]] +
d[[4, 2]] d[[5, 3]] + d[[1, 5]] d[[5, 4]] +
d[[4, 3]] d[[5, 4]] + d[[1, 1]] d[[5, 5]] +
d[[4, 4]] d[[5, 5]]) +
w1 (d[[1, 1]] d[[2, 1]] + d[[3, 1]] d[[2, 1]] +
d[[1, 2]] d[[2, 2]] + d[[1, 3]] d[[2, 3]] +
d[[1, 4]] d[[2, 4]] + d[[1, 5]] d[[2, 5]] +
d[[2, 2]] d[[3, 2]] + d[[2, 3]] d[[3, 3]] +
d[[2, 4]] d[[3, 4]] + d[[2, 5]] d[[3, 5]] +
d[[3, 1]] d[[4, 1]] + d[[3, 2]] d[[4, 2]] +
d[[3, 3]] d[[4, 3]] + d[[3, 4]] d[[4, 4]] +
d[[3, 5]] d[[4, 5]] + d[[1, 1]] d[[5, 1]] +
d[[4, 1]] d[[5, 1]] + d[[1, 2]] d[[5, 2]] +
d[[4, 2]] d[[5, 2]] + d[[1, 3]] d[[5, 3]] +
d[[4, 3]] d[[5, 3]] + d[[1, 4]] d[[5, 4]] +
d[[4, 4]] d[[5, 4]] + d[[1, 5]] d[[5, 5]] +
d[[4, 5]] d[[5, 5]]) +
w2 (d[[1, 1]] d[[1, 2]] + d[[1, 3]] d[[1, 2]] +
d[[1, 3]] d[[1, 4]] + d[[1, 1]] d[[1, 5]] +
d[[1, 4]] d[[1, 5]] + d[[2, 1]] d[[2, 2]] +
d[[2, 2]] d[[2, 3]] + d[[2, 3]] d[[2, 4]] +
d[[2, 1]] d[[2, 5]] + d[[2, 4]] d[[2, 5]] +
d[[3, 1]] d[[3, 2]] + d[[3, 2]] d[[3, 3]] +
d[[3, 3]] d[[3, 4]] + d[[3, 1]] d[[3, 5]] +
d[[3, 4]] d[[3, 5]] + d[[4, 1]] d[[4, 2]] +
d[[4, 2]] d[[4, 3]] + d[[4, 3]] d[[4, 4]] +
d[[4, 1]] d[[4, 5]] + d[[4, 4]] d[[4, 5]] +
d[[5, 1]] d[[5, 2]] + d[[5, 2]] d[[5, 3]] +
d[[5, 3]] d[[5, 4]] + d[[5, 1]] d[[5, 5]] +
d[[5, 4]] d[[5, 5]])], CompilationTarget -> "C",
CompilationOptions -> {"InlineExternalDefinitions" -> True},
RuntimeAttributes -> {Listable}, Parallelization -> True]
res = Table[If[w2 w1 != 0, {w1, w2, 0, 0} -> factorOutRotations[Flatten[Position[#, Min[#]] - 1], 5] &
[ParallelMap[energyCompiled5[#, w1, w2, 0, 0] &, Range[0, 2^25 - 1], {1}]]], {w1, -2, 2}, {w2, -2, 2}]
res1 = Column@DeleteCases[Flatten@res, Null] /. (a_ -> b_) :> a -> Row[ (ArrayPlot[Partition[IntegerDigits[#, 2, 25], 5],
PixelConstrained -> 10] & /@ b)]
