Introduction

My name is Taha Shaikh and I attended the 2017 Wolfram Alpha High School Summer Camp. At this camp, I researched and created a project about many-valued logic.

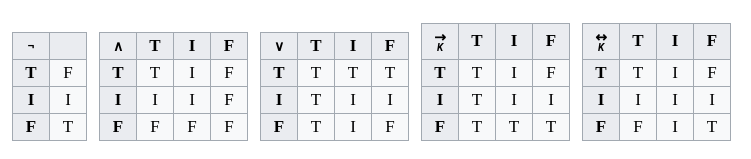
In this exploration, I implemented multivalued logic with the Wolfram language. Multivalued logic is a branch of propositional calculus in which there are more than two truth values. Multivalued logic contrasts with traditional two-valued logic in which only two truth values exist: True and False. The most popular types of many-valued logic are three-valued Kleene and Priest logic, which incorporate an additional Indeterminate value. The truth function for conjunction, for example, is given by:

Procedure

The first step in this project was understanding the aim of the investigation and doing research on the topics at hand. Next, support for the new truth value Undecided was added to the basic boolean operations. I used Kleene and Priest logic tables to redefine the boolean operations.

Undecided = Undecided;
Unprotect[And];
And[Undecided, True] := Undecided
And[Undecided, Undecided] := Undecided
Protect[And];
Unprotect[Boole];
Boole[Undecided] := 0
Boole[False] := -1
Protect[Boole];
Unprotect[Or];
Or[Undecided, False] := Undecided
Or[Undecided, Undecided] := Undecided
Protect[Or];
Unprotect[Not];
Not[Undecided] := Undecided
Unprotect[Implies];
Implies[True, Undecided] := Undecided
Implies[Undecided, Undecided] := True
Implies[False, Undecided] := True
Implies[Undecided, True] := True
Implies[Undecided, False] := Undecided
Protect[Implies];
Unprotect[Nand];
Nand[Undecided, Undecided] := Undecided
Protect[Nand];
Unprotect[Nor];
Nor[Undecided, Undecided] := Undecided
Protect[And];

These functions ensured that the rest of the functions created worked smoothly. The next step was creating a function that would generate truth tables based on a given operation and the list of the variables used. The TernaryTable function used an input of a logic expression and the list of used variables and converts it into a truth table. Where Boolean logic has $2^2 = 4$ unary operators, the addition of a third value in ternary logic leads to a total of $3^3 = 27$ distinct operators on a single input value. It uses the Tuples function to run through all of the possible permutations of the three truth values and runs them through the given expression.

TernaryTable[expr_, vars__] :=

 ReplaceAll[expr, Thread[vars -> #]] & /@ 
  Tuples[{True, False, Undecided}, {Length[vars]}]

An example of TernaryTable in action:

This function uses the Tuples function to run through the various combinations and permutations of the three different truth values. The truth table generated has length $3^n$ in which $n$ is the number of variables used in the logic expression. In the case of this example, since four variables are present (x, y, z, w), the length of its truth table is $3^4$ or 81. This is because all possible permutations of the three truth values are considered when generating the truth table. Even though many of the outputs are the same, their individual logic expressions were unique. Creating a function that created truth tables was a good first step and helped me better visualize and understand the topic.

Cooking Up Some Functions

The main strategy for determining the identity of the truth table was brute-force-esque. All of the possible arrangements of the basic logic functions were ran through the tuples of the three logic values. Their logic expression was also calculated and correlated to their truth table. First, I made a function called LotsOfTernaryTables that produces a lot of ternary tables. Given the number of variables, it produces every possible truth table for every possible arrangement of the functions And, Or, Nand, Nor, and Not for the given variables.

LotsOfTernaryTables[x_] :=

  MatrixForm[
   Groupings[#, {And -> 2, Or -> 2, Nand -> 2, Nor -> 2, Not -> 1}, 
      HoldForm] & /@ Tuples[{True, False, Undecided}, {x}]]

In this function, Groupings was used in coordination with Tuples to produce a huge number of different tables.

In order to visualize these massive tables, I created a function called TernaryPlot that generates a colorful plot of the different logic truth tables. It converts the outputs from LotsOfTernaryTables into numerical values and creates a colorful array plot. It uses similar mechanics to the previous function.

TernaryPlot[x_] :=

 ArrayPlot[
  Boole[Groupings[#, {And -> 2, Or -> 2, Nand -> 2, Nor -> 2, 
       Not -> 1}]] & /@ Tuples[{True, False, Undecided}, {x}], 
  ColorRules -> {1 -> Green, 0 -> LightBlue, -1 -> Red}]

The array plot created by this function has several visible patterns and sequences and makes very interesting art. A ternary plot with 3 variables, for example, looks like so:


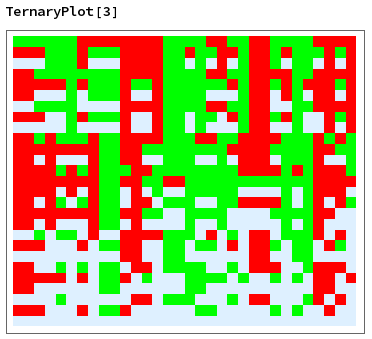
In this plot, every column represents an individual truth table. In this case, since there are three variables, each column contains $3^3=27$ values. When creating ternary plots with more variables, patterns become crazier and the resulting image has some pretty appealing qualities. The ternary plot for 6 variables looks like so:

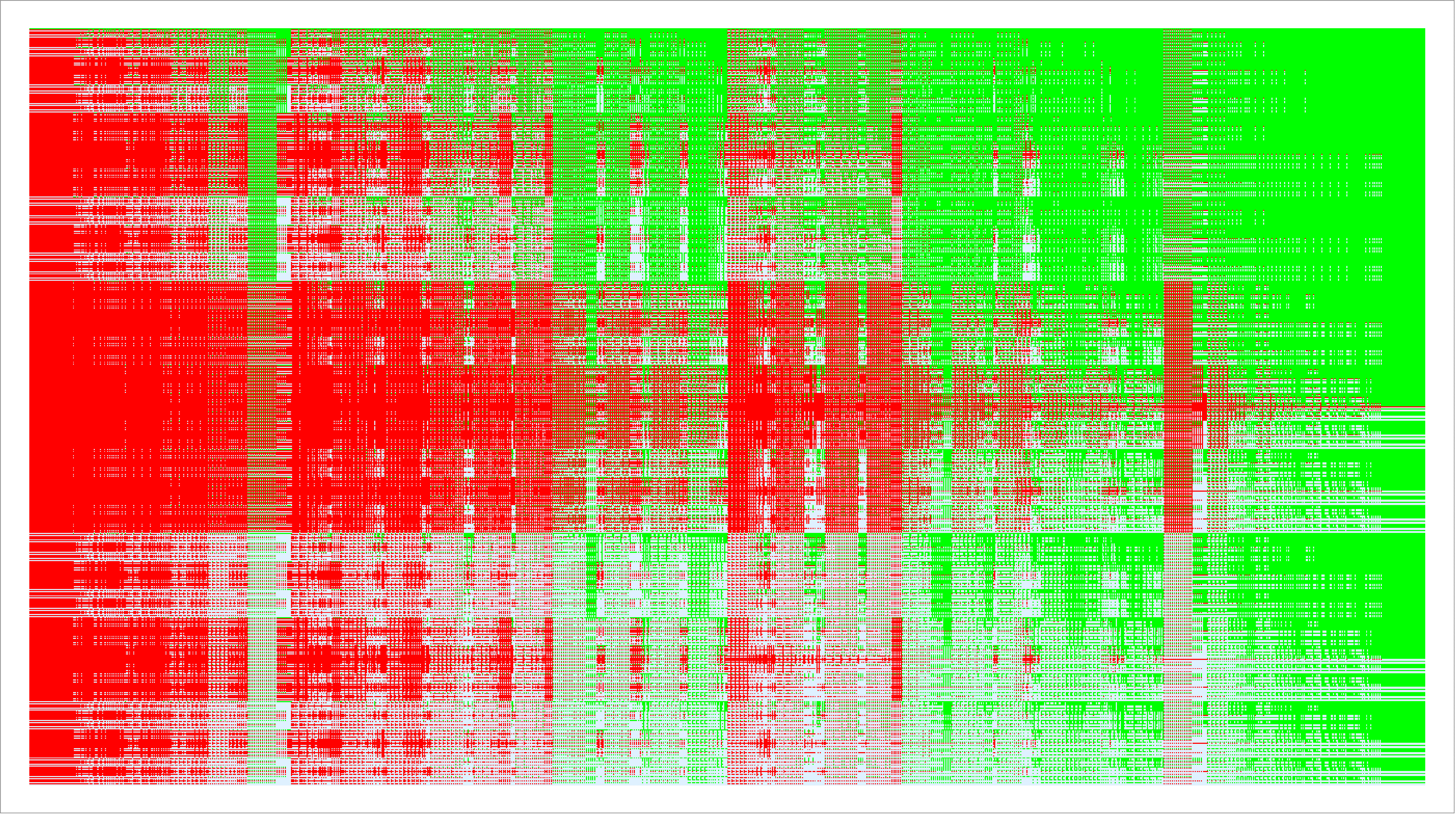
Finally, the last function I created was called TernaryFunction and was based off of the pre-existing BooleanFunction. When given a ternary truth table, this function would return the logic expression associated with it. After generating a list of truth tables and a list of logic expressions, the two lists were then correlated with each other. After retrieving the correct truth table, its corresponding logic expression was derived and returned. In order to assist with this process, the logarithm base 3 of the length of the truth table was calculated and used to narrow down the number of arguments that had to be processed. The function still works with an unlimited number of arguments as long as $log_3n$ is an integer with $n$ representing the length of the inputted truth table.

This is an example of TernaryFunction in action:

The logic function is returned with the given variables as defined by the user.

Differences From Binary Logic

Multi-valued logics are intended to preserve the property of designationhood, or being designated. Since there are more than two truth values, rules of inference may be intended to preserve more than just whichever corresponds to truth. For example, in a three-valued logic, sometimes the two greatest truth-values (when they are represented as e.g. positive integers) are designated and the rules of inference preserve these values. Precisely, a valid argument will be such that the value of the premises taken jointly will always be less than or equal to the conclusion.

Applications of Ternary Logic

An application of many valued logic is geared towards the design of electronic circuits which employ more than two discrete levels of signals, such as many-valued memories, arithmetic circuits, and field programmable gate arrays. Many-valued circuits have a number of theoretical advantages over standard binary circuits. For example, the interconnect on and off chip can be reduced if signals in the circuit assume four or more levels rather than only two. In memory design, storing two instead of one bit of information per memory cell doubles the density of the memory in the same die size. Applications using arithmetic circuits often benefit from using alternatives to binary number systems. For example, residue and redundant number systems can reduce or eliminate the ripple-through carries which are involved in normal binary addition or subtraction, resulting in high-speed arithmetic operations.

Attachments: