Why this question affects my choice of finite element solver

In my project, I am importing a complex geometry from an STL file into Mathematica as a MeshRegion. I would like to edit this mesh significantly: For instance, drastically reduce or increase the number of elements (for finite element analysis) or make boolean operations. But I am not sure if Mathematica can re-mesh a MeshRegion that is obtained from discrete data. This question is of personal importance for me because it will help decide if I can go ahead with using NDSolve for the finite element analysis of my project: If re-meshing is very problematic in Mathematica, it may be wiser to import volume meshes from external software, or do all of the finite element analysis in a dedicated solver like Comsol.

Re-meshing an already discretized MeshRegion

Let me illustrate. When I work with an ImplicitRegion, I seem to have full control, I can make a mesh with very many or few elements, and apply boolean operations too:

IR = ImplicitRegion[
   x^6 - 5 x^4 y + 3 x^4 y^2 + 10 x^2 y^3 + 3 x^2 y^4 - y^5 + y^6 + 
     z^2 <= 1, {x, y, z}];
<< NDSolve`FEM`
ToElementMesh[IR, MaxCellMeasure -> Infinity, 
  AccuracyGoal -> 0]["Wireframe"]
ToElementMesh[RegionDifference[IR, Cuboid[]], 
  MaxCellMeasure -> 0.001]["Wireframe"]

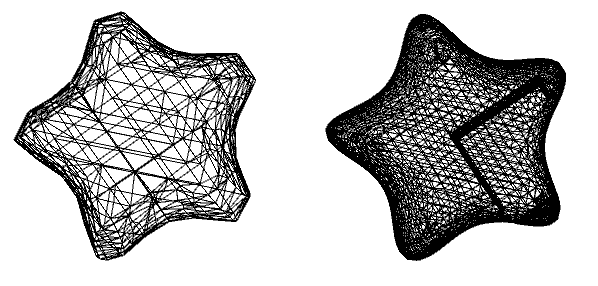
Next, I create a MeshRegion by applying DiscretizeRegion. This leaves me in basically the same situation as importing some STL mesh into Mathematica as MeshRegion:

MR = DiscretizeRegion[IR]; (* same as MR = Import["filename.stl", "MeshRegion"] *)

Now I can no longer downsample:

ToElementMesh[MR, MaxCellMeasure -> Infinity, AccuracyGoal -> 0]
ToElementMesh[MR]

Same thing! No downsampling appears to have happened. Possibly no re-meshing whatsoever. Mathematica returns basically the same number of elements (TetrahedronElement["<" 16793 ">"] vs TetrahedronElement["<" 16841 ">"], respectively).

Also I can no longer apply boolean operations:

RegionDifference[MR, Cuboid[]] // DiscretizeRegion

returns an error

Is there some way I could gain control of the DiscretizeRegion in the same way as ImplicitRegion? In practice, I am presented with discrete data (STL file) and I would like to be able to re-mesh it, do boolean operations, and run FEM in full control of my mesh. Is that possible?

Bad brute force solution

You can brute force Mathematica to re-mesh using this hack:

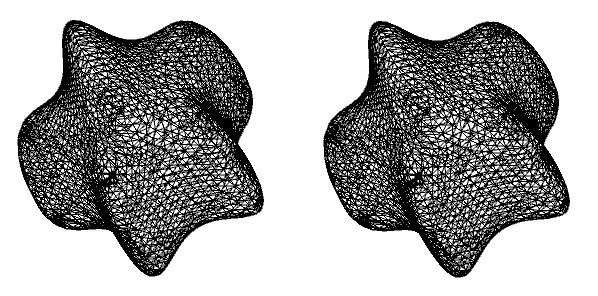
    MR2 = DiscretizeGraphics[
      RegionPlot3D[
       RegionMember[MR, {x, y, z}] == True && 
        RegionMember[Cuboid[], {x, y, z}] == False, {x, -2, 2}, {y, -2, 
        2}, {z, -2, 2}, PlotPoints -> 20]]
ToElementMesh[MR2, MaxCellMeasure -> Infinity, AccuracyGoal -> 0]

However, converting the MeshRegion (picture above, left) with ToElementMesh hopelessly overmeshes things (picture above, right). I get about 500k tetrahedral elements. Once again I don't know how to control my mesh for finite element analysis.

Disclaimer

I have posted this question to Mathematica Stackexchange here, where it has gone unanswered for several days. Because of the importance of this question for my modeling work (I need to decide if I can go ahead with Mathematica for the finite element analysis part of my project), I decided to post it to the Wolfram Community to hopefully get some developer feedback. I am happy to summarise the insights of this this discussion for the Stackexchange community once we have (hopefully) reached some conclusions.