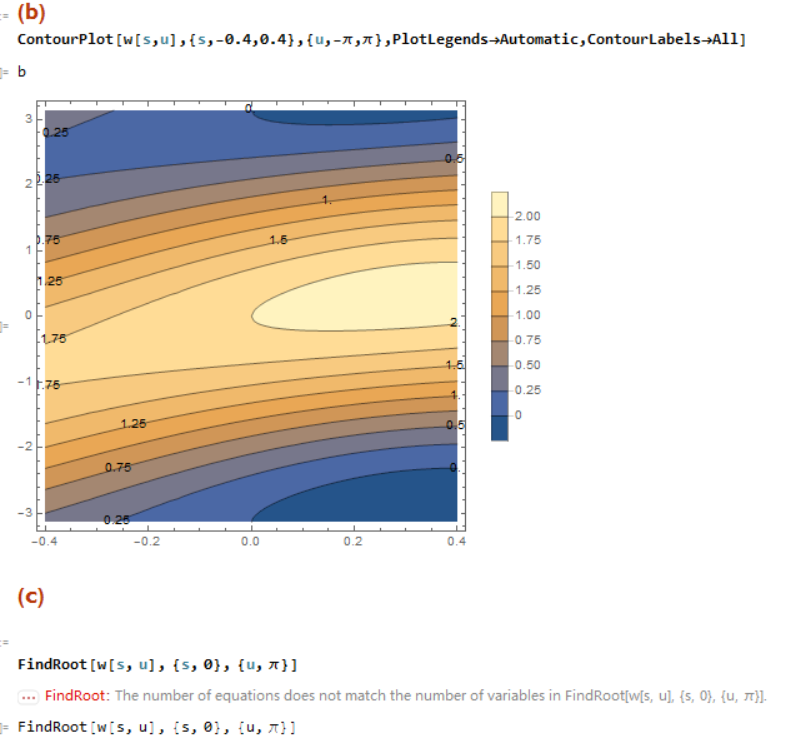
I have this equation :

w[s_, u_] := 1 + (1 + 0.65 s - 1.2 s^2 - 0.4 s^3 + 0.35 s^4) Cos[u] + (1.4 s - 0.4 s^2 - 1.5 s^3 - 0.35 s^4) Sin[u];

And I need to find the critical point of this equation; The requirement is using the ContourPlot and FindRoot to solve it, so I need to give the FindRoot function an initial guess for a critical point; I can see the initial guess now, but how to find the "Find Root function" ?

If I try:

FindRoot[w[s, u], {s, 0}, {u, pi}]

,then the error message: " The number of equations does not match the number of variables in FindRoot[w[s,u],{s,0},{u,[Pi]}]."

Please help, Thank you!