Message Boards Message Boards

0
|
6447 Views
|
4 Replies
|
2 Total Likes
View groups...
Share
Share this post:

[?] Plot gradient of a function of a variable?

Gennaro Arguzzi
Posted 7 years ago

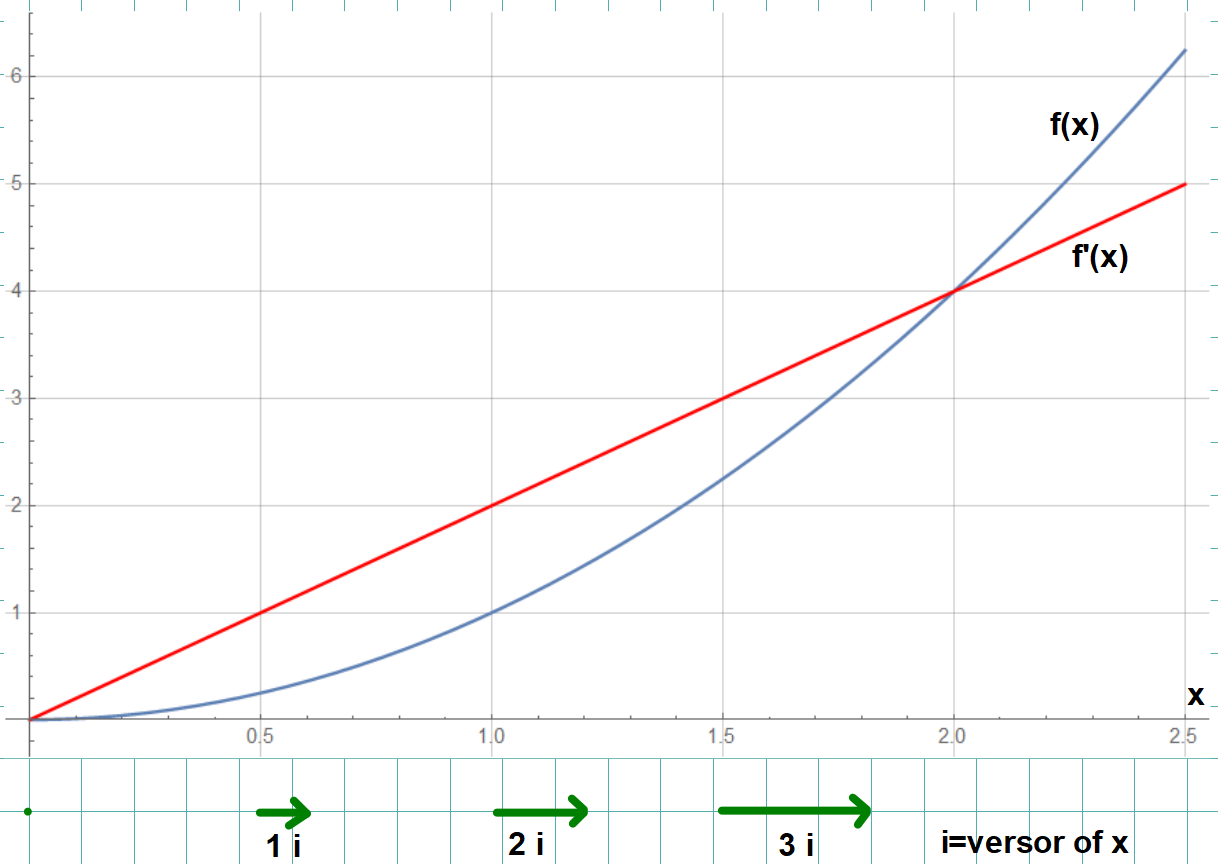
Hello everyone, I'd like to plot the gradient of a function of a variable. Before I hope that the derivative is the component of the gradient, that is a scalar, instead the gradient is a vector. For example, for the function f(x)=x^2 and f'(x)=2x, the gradient should be the plot with green arrows:

enter image description here

I tried to do it with the following statement:

VectorPlot[{2 x, 0}, {x, -3, 3}, {y, 0, 0.00001}]

Is it correct?

When I try to plot f(x), f'(x) and gradient, I get a strange plot because maybe the range {y, 0, 0.00001} in VectorPlot does not allow to show me the range I set:

Show[VectorPlot[{2 x, 0}, {x, 0, 2.5}, {y, 0, 0.00001}], 
 Plot[x^2, {x, 0, 2.5}, PlotRange -> {{0, 2.5}, {0, 6}}], 
 Plot[2 x, {x, 0, 2.5}, PlotRange -> {{0, 2.5}, {0, 6}}, 
  PlotStyle -> Red]]

Thank you so much for your time.
POSTED BY: Gennaro Arguzzi
4 Replies
Sort By:

Your plot is strange perhaps because VectorPlot displays many rows of arrows, which are almost superimposed in your composite plot. Unfortunately VectorPlot does not allow a single row of arrows, it wants at least two:

VectorPlot[{2 x, 0}, {x, 0, 2.5}, {y, 0, 0.00001}, 
 VectorPoints -> {7, 1}]

Here is a workaround that collects with Cases a single row of arrows from VectorPlot and displays it as an Epilog:

Plot[{x^2, 2 x}, {x, 0, 2.5}, PlotRange -> {{0, 2.7}, {-1.1, 7}}, 
 PlotStyle -> {Automatic, Red}, 
 Epilog -> 
  Translate[
   Cases[VectorPlot[{2 x, 0}, {x, 0, 2.5}, {y, 0, 0.00001}, 
     VectorPoints -> {7, 2}], Arrow[{{_, 0.}, _}], All], {0, -1}]]
POSTED BY: Gianluca Gorni

Thank you for your help @Gianluca Gorni .
POSTED BY: Gennaro Arguzzi

"Gradient" usually refers to the situation of a scalar-valued function of a vector variable, which typically means the domain is a subset of Rn for n ≥ 2.

In your example, by "gradient" do you simply mean the slope of the real-valued function of one real variable?
POSTED BY: Murray Eisenberg

Hello @Murray Eisenberg , yes I mean the vector given by the product between angular coefficient of the tangent and the versor i because I know that in this special case I can define gradient also for function of a variable:

nabla(f) = (df/dx,0,0) = df/dx i
POSTED BY: Gennaro Arguzzi
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract