Group Abstract Group Abstract

Message Boards Message Boards

0
|
10.2K Views
|
6 Replies
|
3 Total Likes
View groups...
Share
Share this post:

[?] Solve a cubic equation?

Metin Guney
Posted 8 years ago

Please look at this outcome:

enter image description here

As you see, all 3 roots are complex numbers. But this equition has a real root at least 1. This is 0.1736 ... (exactly sin 10 degrees).

enter image description here

Where is my fault?

POSTED BY: Metin Guney
6 Replies
Sort By:
Metin Guney
Metin Guney
Posted 8 years ago

"Casus irreducibilus" explained everything. Thank you for detailed explanations.
POSTED BY: Metin Guney

(1) Please post actual code rather than an image of code.

(2) Have a look at the casus irreducibilus.

(3) One can avoid seemingly complex radicals in the result using an option setting to disable the Cardano/Tartaglia cubic form of result.

InputForm[Solve[(8*t^3 - 6*t + 1 == 0), t, Cubics->False]]              

(* Out[2]//InputForm= 
{{t -> Root[1 - 6*#1 + 8*#1^3 & , 1, 0]}, 
 {t -> Root[1 - 6*#1 + 8*#1^3 & , 2, 0]}, 
 {t -> Root[1 - 6*#1 + 8*#1^3 & , 3, 0]}} *)

N[%]                                                                    

(* Out[3]= {{t -> -0.939693}, {t -> 0.173648}, {t -> 0.766044}} *)

Alternatively convert the cubic radicals to trigs.

InputForm[ComplexExpand[Solve[(8*t^3 - 6*t + 1 == 0), t]]]              

(* Out[5]//InputForm= 
{{t -> Cos[Pi/9]/2 + (Sqrt[3]*Sin[Pi/9])/2}, 
 {t -> Cos[Pi/9]/2 - (Sqrt[3]*Sin[Pi/9])/2}, {t -> -Cos[Pi/9]}} *)
POSTED BY: Daniel Lichtblau

Mathematica is a mathematical program that performs computations on complex numbers(complex plain) and therefore we see the imaginary unit I everywhere.

If You want solution try with ComplexExpand :

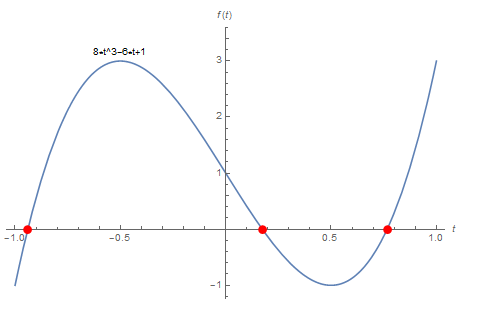
sol = Solve[8*t^3 - 6*t + 1 == 0, t] // ComplexExpand
(* {{t -> 1/2 Cos[\[Pi]/9] + 1/2 Sqrt[3] Sin[\[Pi]/9]}, {t -> 
1/2 Cos[\[Pi]/9] - 1/2 Sqrt[3] Sin[\[Pi]/9]}, {t -> -Cos[\[Pi]/9]}} *)

sol//N
(* {{t -> 0.766044}, {t -> 0.173648}, {t -> -0.939693}} *)

Yours equation has 3 real roots:

Plot[8*t^3 - 6*t + 1, {t, -1, 1}, Epilog -> {Red, PointSize[0.02], Point[{t /. sol[[#]] // N, 0} & /@ {1, 2, 3}]}, 
AxesLabel -> {t, f[t]}, PlotLabels -> Placed[{"8*t^3-6*t+1"}, Above]]

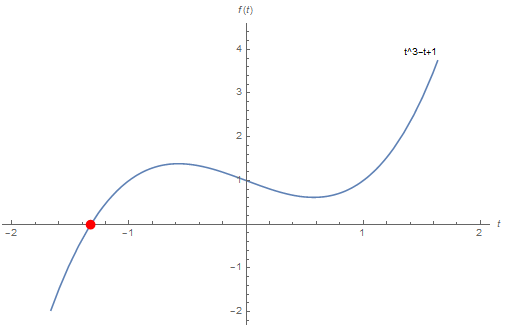
enter image description here

Another example with 1 real and 2 complex roots:

sol1 = Solve[t^3 - t + 1 == 0, t] // ComplexExpand
(* {{t -> -(2/(3 (9 - Sqrt[69])))^(1/3) - (1/2 (9 - Sqrt[69]))^(1/3)/3^(
    2/3)}, {t -> (1/2 (9 - Sqrt[69]))^(1/3)/(2 3^(2/3)) + 1/(
    2^(2/3) (3 (9 - Sqrt[69]))^(1/3)) + 
    I (-(3^(1/6)/(2^(2/3) (9 - Sqrt[69])^(1/3))) + (9 - Sqrt[69])^(
       1/3)/(2 2^(1/3) 3^(1/6)))}, {t -> (1/2 (9 - Sqrt[69]))^(1/3)/(
    2 3^(2/3)) + 1/(2^(2/3) (3 (9 - Sqrt[69]))^(1/3)) + 
    I (3^(1/6)/(2^(2/3) (9 - Sqrt[69])^(1/3)) - (9 - Sqrt[69])^(1/3)/(
       2 2^(1/3) 3^(1/6)))}}*)
sol1 // N
(* {{t -> -1.32472}, {t -> 0.662359 - 0.56228 I}, {t -> 0.662359 + 0.56228 I}} *)

Plot[t^3 - t + 1, {t, -2, 2}, Epilog -> {Red, PointSize[0.02], 
Point[{t /. sol1[[#]] // N, 0} & /@ {1}]}, AxesLabel -> {t, f[t]}, PlotLabels -> Placed[{"t^3-t+1"}, Above]]

enter image description here
POSTED BY: Mariusz Iwaniuk
Metin Guney
Metin Guney
Posted 8 years ago

Thanks for detailed explanations.
POSTED BY: Metin Guney

You can use NSolve:

NSolve[(8*t^3 - 6*t + 1 == 0), t]

This gives {{t -> -0.939693}, {t -> 0.173648}, {t -> 0.766044}}

For exact solutions:

ComplexExpand@Solve[(8*t^3 - 6*t + 1 == 0), t]
POSTED BY: Priyan Fernando
Metin Guney
Metin Guney
Posted 8 years ago

Thanks for your explanations. But what I can't understand is the behavior of Mathematica. Is this equition has more than 3 roots, 3 of them are real, other 3 are complex?
POSTED BY: Metin Guney
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard