Hi, again.
The problem is this:
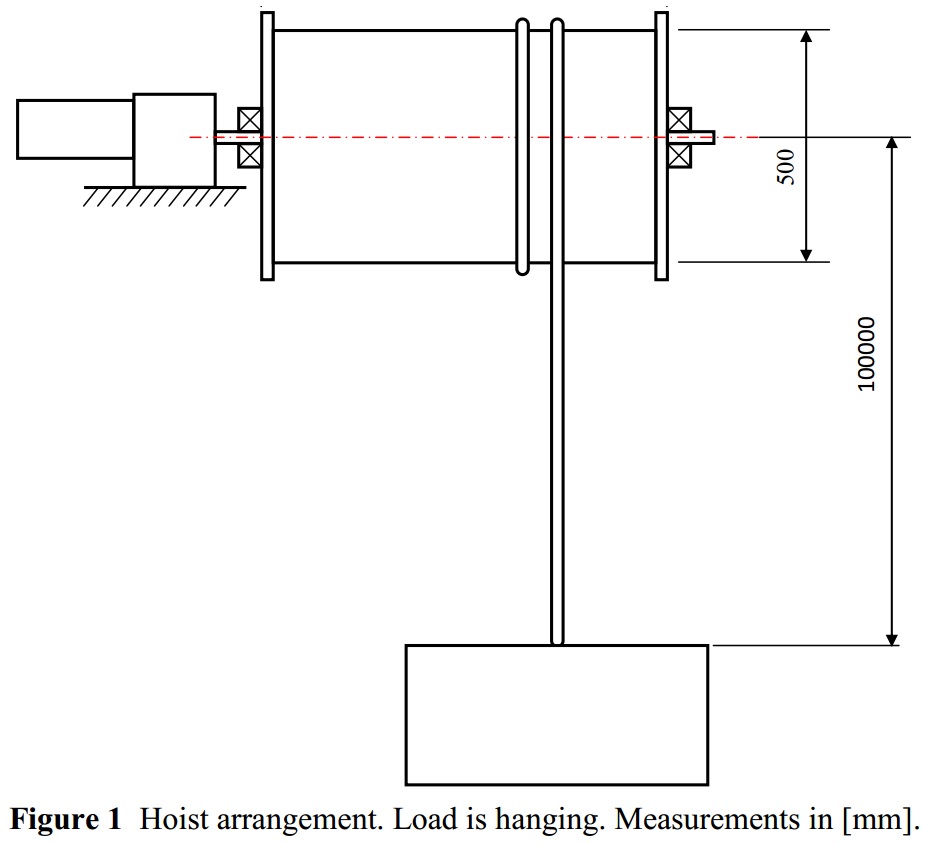
I want to simulate the motion of the load given the following Torque profile from the motor:
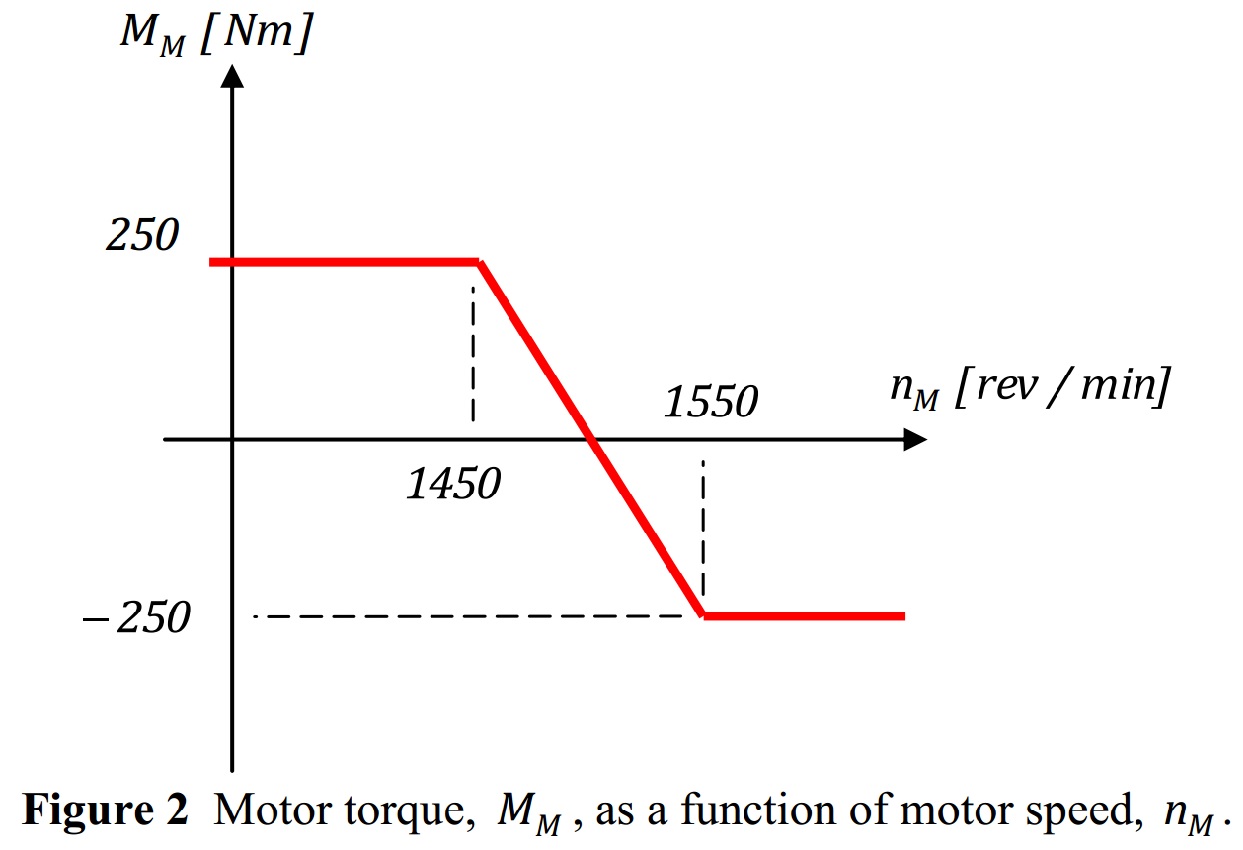
How do I define this parametric torque function (given the fact that it's a function of angular velocity) and then use it to solve differential equations?
What I have tried so far: Defining M as parametric function and defining events for the values of M in DSolve environment:
Subscript[J, M] := 0.16
n := 5
r := 250/1000
Subscript[J, d] := 7.2
m := 180
g := 9.81
Subscript[M, M][Subscript[\[Theta], M]'[t_]] :=
Piecewise[{{250,
Subscript[\[Theta], M]'[t] <= 151.84}, {250 -
47 Subscript[\[Theta], M]'[t],
151.84 < Subscript[\[Theta], M]'[t] < 162.316}, {-250,
Subscript[\[Theta], M]'[t] >= 162.316}}];
system = NDSolve[{(Subscript[J, M] + Subscript[J, d]/
n^2) Subscript[\[Theta], M]''[t] ==
Subscript[M, M] - (m g r)/n,
m y''[t] == (Subscript[M, M] n)/r - m g, y[0] == 0, y'[0] == 0,
Subscript[\[Theta], M]'[0] == 0, Subscript[\[Theta], M][0] == 0},
y, {t, 0, 5}]
system = NDSolve[{(Subscript[J, M] + Subscript[J, d]/
n^2) Subscript[\[Theta], M]''[t] ==
Subscript[M, M] - (m g r)/n,
m y''[t] == (Subscript[M, M] n)/r - m g, y[0] == 0, y'[0] == 0,
Subscript[\[Theta], M]'[0] == 0, Subscript[\[Theta], M][0] == 0,
WhenEvent[Subscript[\[Theta], M]'[t] <= 151.84,
Subscript[M, M] -> 250],
WhenEvent[
Subscript[\[Theta], M]'[t] > 151.84 &&
Subscript[\[Theta], M]'[t] < 162.316,
Subscript[M, M] -> 250 - 47 Subscript[\[Theta], M]'[t]],
WhenEvent[Subscript[\[Theta], M]'[t] >= 162.316,
Subscript[M, M] -> -250]}, y, {t, 0, 5}]
Sorry about the messy code.
Screen:

Thanks for any help.