I do not see a problem there. If I discretize it like:

Clear[mu0, a, b, c, gap, R]
a = b = c = 0.01; gap = 0.00106; R = 0.1; mu0 = 10^6;
lsttnqvrbmmf = 
  ParallelTable[{{x1, y1, z1}, 
    tnqvrbmmf[mu0, a, b, c, x1, y1, z1]}, {x1, -1.5*a, 
    5.5*a + 4.0*gap, gap}, {y1, -2.0*b, 2.0*b, gap}, {z1, -3.5*c, 
    1.5*c + R, gap}]  ;

and display the data with `ListVectorPlot3D`, I am getting the same kind of plot.

ListVectorPlot3D[lsttnqvrbmmf, VectorPoints -> {40, 20, 30}, 
BoxRatios -> Automatic, Axes -> True, PlotLegends -> Automatic, 
PlotRange -> {{-0.015, 0.059}, {-0.02, 0.02}, {-0.035, 0.115}}]

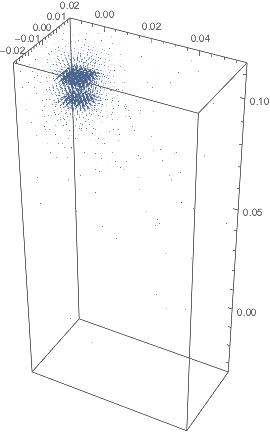
so, I still suspecting that the TransformedField-ed field is somewhat different for VectorPlot3D than was the original and that can cause problems for ReplaceAll, does not matter how I do want to employ it, PostFix or not.