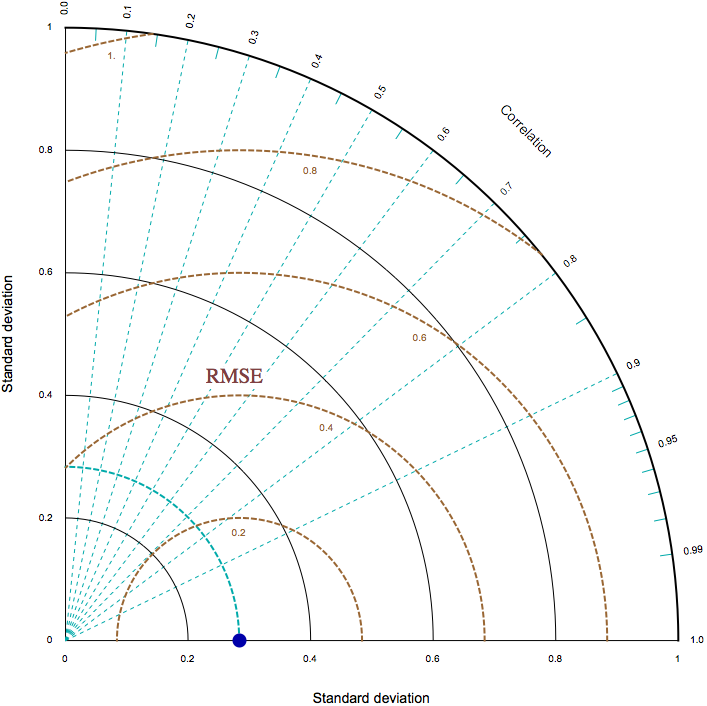
Dear all, I would like to know, how I can mark the position of a point with following coordinates:
Correlarion= 0.7 , Standard Deviation= 0.55 and RMSE=0.4.
Many thanks for your help.
maxsize=1;
arcinterval=maxsize/5.0;
ticksize=0.02;
frameticksoffset=0.02;
label="Standard deviation";
corrlabel="Correlation";
radialcolor=Darker@Cyan;
observedcolor=Darker@Blue;
rmsarccolor=Brown;
ClearAll[RadialLine,RadialPosition]
RadialLine[corr_?NumericQ]:={{0,0},RadialPosition[corr]}
RadialPosition[corr_?NumericQ]:=AngleVector[{maxsize,ArcCos[corr]}]
arcs=Circle[{0,0},#,{0,Pi/2}]&/@Range[maxsize,0,-arcinterval];
arcs[[1]]={Thick,arcs[[1]]};
radial={{Black,Line[RadialLine/@{0,1}]},{radialcolor,Dashed,Line[RadialLine/@Range[0.1,0.9,0.1]]}};
tickmarks=RadialPosition/@Join[Range[0.05,0.85,0.1],Range[0.91,0.99,0.01]];
tickmarks= {#,(1-ticksize)#}&/@tickmarks;
tickmarks={radialcolor,Line[tickmarks]};
frameticks=Range[0,1,0.1]~Join~{0.95,0.99};
frameticklabels=If[Round[#,0.1]==#,NumberForm[#,{\[Infinity],1}],#]&/@frameticks;
frameticks=MapThread[Text[#1,(1+frameticksoffset)#2,{-1,0},AngleVector[#3]]&,
{frameticklabels,RadialPosition/@frameticks,ArcCos[frameticks]}];
axesticks=Range[maxsize,0,-arcinterval];
axesticks=Join[Text[If[Round[#]==#,Round[#],#],{#,-maxsize frameticksoffset},{0,1}]&/@axesticks,
Text[If[Round[#]==#,Round[#],#],{-maxsize frameticksoffset,#},{1,0}]&/@axesticks];
framelabels={
Text[Style[label,14],{maxsize/2,-4maxsize frameticksoffset},{0,1}],
Text[Style[label,14],{-4maxsize frameticksoffset,maxsize/2},{0,-1},{0,1}],
Text[Style[corrlabel,14],AngleVector[{(1+6frameticksoffset)maxsize,45\[Degree]}],{1,0},AngleVector[-45\[Degree]]]
};
origin=StandardDeviation[observed];
datapoints={{observedcolor,PointSize[0.02],Point[{origin,0}]}};
meanarc={radialcolor,Thick,Dashed,Circle[{0,0},origin,{0,Pi/2}]};
ClearAll[CreateRMSarcs]
CreateRMSarcs[origin_,arcsize_,maxsize_]:=Module[{start,stop},
start=If[origin+arcsize>maxsize,
Pi-ArcCos[(maxsize^2-arcsize^2-origin^2)/(-2arcsize origin)]
,0];
stop=If[origin-arcsize>=0,Pi,
Pi-ArcCos[origin/arcsize]];
{Dashed,Thick,rmsarccolor,Circle[{origin,0},arcsize,{start,stop}],
Text[arcsize,AngleVector[{origin,0},{arcsize-0.025maxsize,(stop+start)/2}]]}
]
rmsarcs=CreateRMSarcs[origin,#,maxsize]&/@Range[0.2,1.0,0.2];
Graphics[{radial,tickmarks,arcs,frameticks,axesticks,framelabels,meanarc,datapoints,rmsarcs}]
 Attachments:
Attachments: