HI, I have a vector field in a form of mHi3ret[x,y,z}={f[x,y,z],g[x,y,z],h[x,y,z]}. I need to integrate the first component f[x,y,z] over a rectangular area. f[x,y,z] is has many tags in different forms of elementary function like:
1. (0. + 1. (-0.1 +
1. (0. +
1.25664*10^-6 (1.05042*10^6 (OutputSizeLimit`Skeleton[1]) +
1.32*10^7 UnitStep[
QuantityMagnitude[
0.000025 - (-0.1 +
1. (0. +
1. (0.1 + OutputSizeLimit`Skeleton[
1])))^2]] UnitStep[
QuantityMagnitude[
0.000025 -
1. (0. +
1. (OutputSizeLimit`Skeleton[1]))^2]] UnitStep[
QuantityMagnitude[
0.000025 - 1. (0. + 1. (0.1 - 1. z))^2]]))) +
1. (OutputSizeLimit`Skeleton[1]) +
1. (OutputSizeLimit`Skeleton[1]) +
1. (0.120359 -
1. (0. - 0.304293 (OutputSizeLimit`Skeleton[1]) +
1.22279*10^-6 (OutputSizeLimit`Skeleton[1]))) +
1. (0. +
1. (0. +
1.24046 (((-0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2)/((-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 OutputSizeLimit`Skeleton[1] -
0.341889 (0. + OutputSizeLimit`Skeleton[
1])))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) - (-0.005 - 1. (0. + 1. (0. + 1. y)))/
Sqrt[(-0.005 - 1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2] - ((0.005 -
1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (OutputSizeLimit`Skeleton[
1]))^2)/((OutputSizeLimit`Skeleton[6] -
OutputSizeLimit`Skeleton[1])^2 +
OutputSizeLimit`Skeleton[
1]^2 + (OutputSizeLimit`Skeleton[1])^2)^(3/2) +
OutputSizeLimit`Skeleton[210] +
Log[0.005 - 1. (0. + 1. (0. + 1. y)) +
Sqrt[(0.005 - 1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2]]) +
4.2963*10^-7 (1.05042*10^6 (((-0.005 -
1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) - ((0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) - ((-0.005 - 1. (0. + 1. (0. + 1. y))) (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) + ((0.005 - 1. (0. + 1. (0. + 1. y))) (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) - ((-0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(
3/2) + ((0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))) (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))))/((0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2)^(3/2) +
OutputSizeLimit`Skeleton[152] +
ArcTan[((0.005 - 1. (0. + 1. (0. + 1. y))) (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))))/((0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))) Sqrt[(0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.095 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2])] -
ArcTan[((-0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))))/((0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))) Sqrt[(-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2])] +
ArcTan[((0.005 - 1. (0. + 1. (0. + 1. y))) (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))))/((0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))) Sqrt[(0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (-0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2])] +
ArcTan[((-0.005 - 1. (0. + 1. (0. + 1. y))) (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))))/((0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))) Sqrt[(-0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2])] -
ArcTan[((0.005 - 1. (0. + 1. (0. + 1. y))) (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))))/((0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z))) Sqrt[(0.005 -
1. (0. + 1. (0. + 1. y)))^2 + (0.005 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z)))^2 + (0.105 -
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. + 1. z)))^2])]) +
1.32*10^7 UnitStep[
QuantityMagnitude[
0.000025 - 1. (0. + 1. (0. + 1. y))^2]] UnitStep[
QuantityMagnitude[
0.000025 -
1. (0. + 0.93974 (0. + 1. x) -
0.341889 (0. + 1. z))^2]] UnitStep[
QuantityMagnitude[
0.000025 - (-0.1 +
1. (0. + 0.341889 (0. + 1. x) +
0.93974 (0. +
1. z)))^2]])))) + OutputSizeLimit`Skeleton[3] +
1. (OutputSizeLimit`Skeleton[1])
So I try to do something like:
mflx = Integrate[
mHi3ret[[1, 1]], {y, -cb/2, cb/2}, {z, R - c/2 - cmg - cb, }] /.
x -> 0.0; // AbsoluteTiming
where
a = b = c = 0.01; R = 0.1; cb = 1.5*b; cc = 2*c; cd = a/20; cn = 10; cmg = c/10;
all are some numerical values. Mathematica runs for hours, eats up good amount of real and virtual memory and ultimately OS X kills it. Here is an Activity Monitor stage after 3 hours of run.
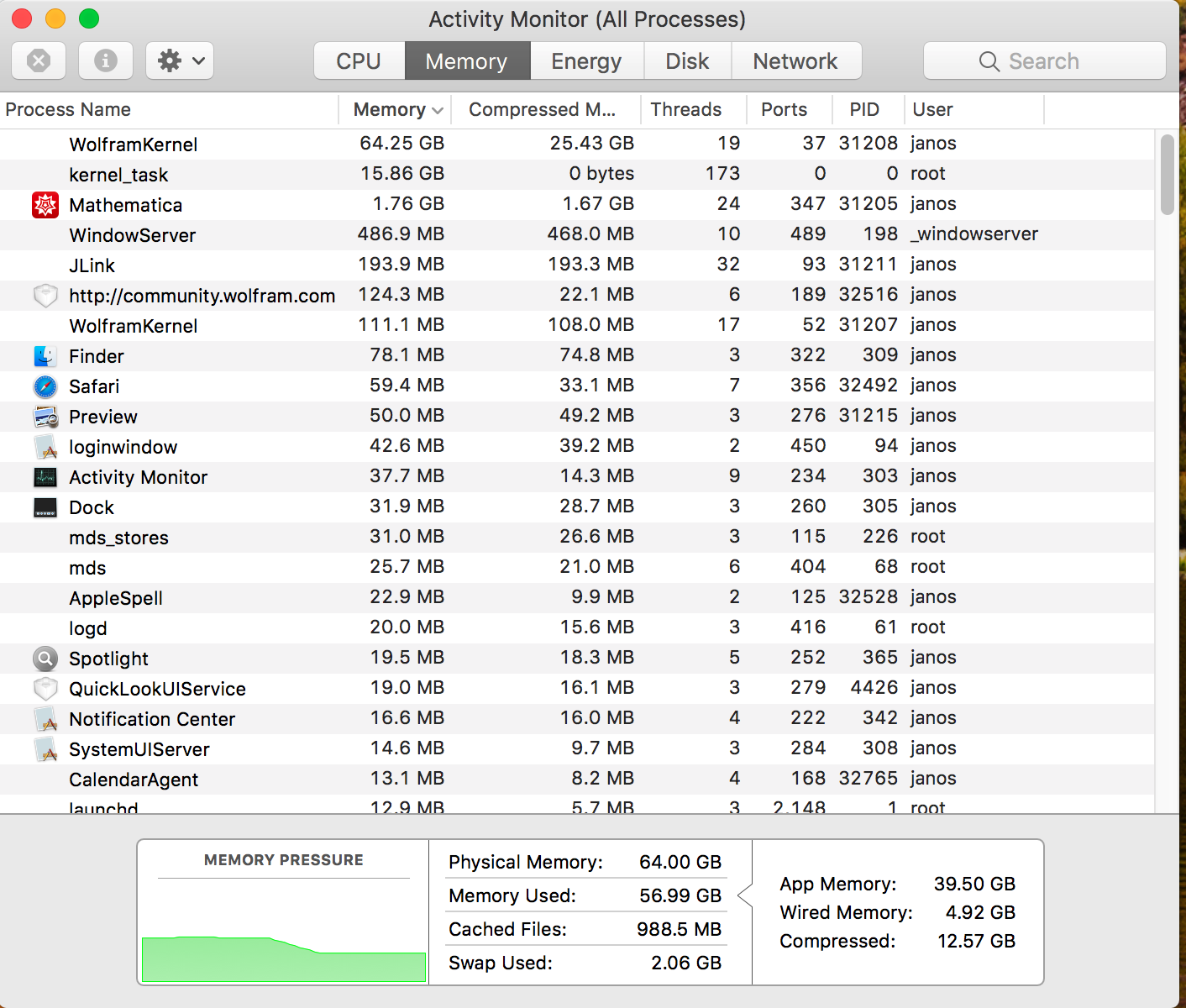
Any good hint to be able to have the Integrate finish its job? Thanks ahead, János