You expect Mathematica to find the continuation because Piecewise says in Examples -> Scope
Integration constants are chosen to make the result continuous:
which is correct in one dimension. In 2 or more dimensions two problems arise (as you found)
- the integral is given only on the actual support of the piecewise function
- it's generally not the job of indefinite
Integrate[] to fix integration constants
But one reaches the intended result without labour:
In[1]:= tent[x_] := Piecewise[{{x + 1, -1 <= x < 0}, {1 - x, 0 <= x <= 1}}]
In[2]:= tent2[x_, y_] := PiecewiseExpand[tent[x] tent[y]]
In[3]:= Clear [stamm]
stamm[x_, y_] := Evaluate[Integrate[tent2[x, y1], y1] /. y1 -> y]
In[5]:= Clear[stammC]
stammC[x_, y_] := stamm[x, y] - If[y < -1, 0, If[y < 1, stamm[x, -1], stamm[x, -1] - stamm[x, 1]]]
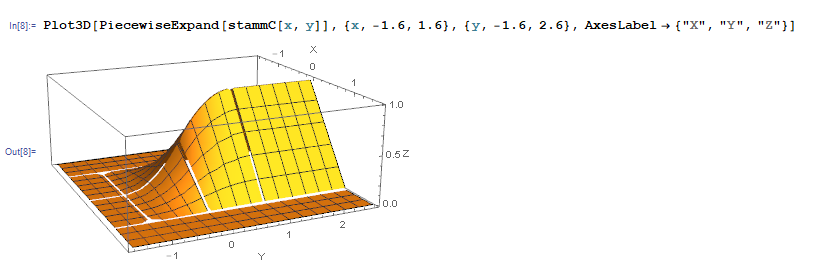
In[8]:= Plot3D[PiecewiseExpand[stammC[x, y]], {x, -1.6, 1.6}, {y, -1.6, 2.6}, AxesLabel -> {"X", "Y", "Z"}]
which is your Plot3D[HyExpected[x, y], {x, -1.6, 1.6}, {y, -1.6, 2.6}, PlotRange -> Full]:
If one muses about it one will see that's in general not easy to find the intended integration constants (Piecewise[] can go in irregular shapes (i.e. not axis-parelle) etc. etc.), but the problem owner can do.