Since it is basketball season (right now we are in the middle of March madness) I thought it'd be fun to make a basketball simulation. Basketball Boids is motivated by the boids model of bird flocks, with a term for separation from teammates, a term for cover/separation from the other team (sign depends on offense or defense), an attraction towards the basket. You can try your own parameters, and you can try other models. Ideally, there would be so-called emergent properties like team work and creativity as in the bird flocks.

Blue is offense and red is defense.

m = Through[{m1, m2, m3, m4, m5}[t]];(*{m1[t],m2[t],m3[t],m4[t],m5[t]}*)
p = Through[{p1, p2, p3, p4, p5}[t]];(*{p1[t],p2[t],p3[t],p4[t],p5[t]}*)

Those are the variables and this solves the differential equation, with the boid parameters in the code. The separation and cover terms are inverse square forces, but the hoop term is just radial.

dm[n_] :=  separation*   Sum[(m[[n]] -  m[[i]])/((m[[n]] - m[[i]]).(m[[n]] - m[[i]]))^(3/2), {i, 5}] +  cover*Sum[(m[[n]] - 
       p[[i]])/((m[[n]] - p[[i]]).(m[[n]] - p[[i]]))^(3/2), {i, 5}] + hoop*(-m[[n]]/(m[[n]].m[[n]])^(1/2))

dp[n_] := separation*Sum[(p[[n]] -  p[[i]])/((p[[n]] - p[[i]]).(p[[n]] - p[[i]]))^(3/2), {i, 5}] - cover*Sum[(p[[n]] - 
       m[[i]])/((p[[n]] - m[[i]]).(p[[n]] - m[[i]]))^(3/2), {i, 5}] +   hoop*(-p[[n]]/(p[[n]].p[[n]])^(1/2))

params={separation -> 1,  cover -> 10, hoop -> 100};

sol = Quiet[NDSolve[Evaluate[N@Flatten[Table[{D[m[[i]], t, t] == dm[i], 
          D[p[[i]], t, t] == dp[i], (D[m[[i]], t] /. t -> 0) == {0, 0}, (D[p[[i]], t] /. t -> 0) == {0, 0}, (m[[i]] /. t -> 0) == RandomReal[1, 2], (p[[i]] /. t -> 0) == RandomReal[1, 2]}, {i, 5}]]/. params],Join[m, p], {t, 0, 1}][[1]]];


ParametricPlot[Evaluate[Join[m, p] /. sol], {t, 0, 1},  PlotStyle -> Join[Table[Blue, 5], Table[Red, 5]]]

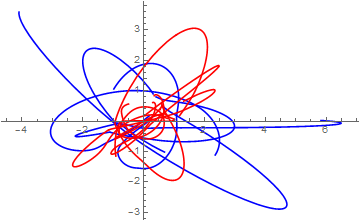
The animation above was made with

Animate[ListPlot[Join[Style[#, Blue] & /@ m, Style[#, Red] & /@ p] /. sol /. t -> s, 
  Axes -> False, Prolog -> {Brown, Disk[{0, 0}, .2]},  AspectRatio -> 1, PlotRange -> 4 {{-1, 1}, {-1, 1}}], {s, 0, 1, .01}]

(I remember talking several years ago to a student at the Wolfram High School Summer Program about Boids, which is why I was thinking about them.)