I will indicate a similar case from which you can get your equation by substituting
$x=\ln {r}, y=\ln {\sin( \phi )}$
x0 = -10; x1 = 1; y0 = -10; y1 = -.01;
eq = {\[CapitalPsi]1[x, y] ==
D[\[CapitalPsi][x, y], x] +
D[\[CapitalPsi][x, y], y], \[CapitalPsi]2[x, y] ==
D[\[CapitalPsi]1[x, y], x] + D[\[CapitalPsi]1[x, y], y], -2*
I*\[CapitalPsi][x, y]*Exp[2*x]/(1 - Exp[2*y])^(5/2) ==
D[\[CapitalPsi]2[x, y], x] +
D[\[CapitalPsi]2[x, y], y], \[CapitalPsi][x0, y] ==
1, \[CapitalPsi]1[x0, y] == 0, \[CapitalPsi]2[x0, y] ==
0, \[CapitalPsi][x1, y] == 1, \[CapitalPsi]1[x1, y] ==
0, \[CapitalPsi]2[x1, y] == 0};
sol = NDSolveValue[eq, \[CapitalPsi], {x, x0, x1}, {y, y0, y1}];
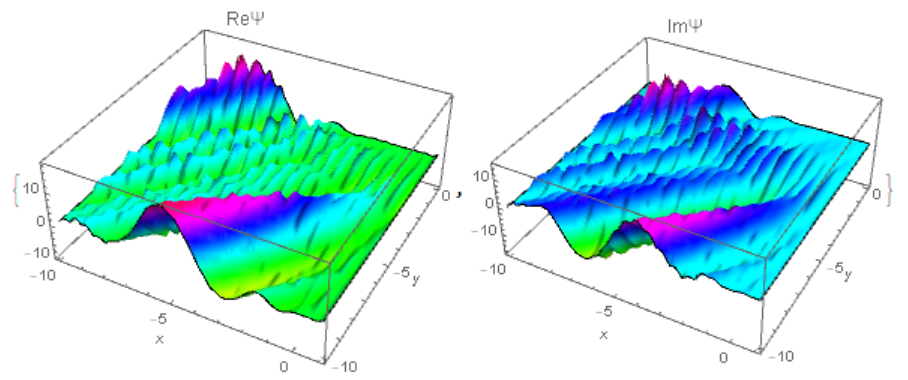
{Plot3D[Re[sol[x, y]], {x, x0, Log[3]}, {y, y0, y1}, PlotRange -> All,
Mesh -> None, ColorFunction -> Hue, MaxRecursion -> 2,
PlotPoints -> 50, AxesLabel -> Automatic,
PlotLabel -> "Re\[CapitalPsi]"],
Plot3D[Im[sol[x, y]], {x, x0, Log[3]}, {y, y0, y1}, PlotRange -> All,
Mesh -> None, ColorFunction -> Hue, MaxRecursion -> 2,
PlotPoints -> 50, AxesLabel -> Automatic,
PlotLabel -> "Im\[CapitalPsi]"]}